Zadanie:
Predstavme si kovovú kružnicu, na ktorej sú rovnomerne rozložené
čísla v poradí
 . Na nej je položená otáčavá drevená kružnica, na ktorej sú
opäť
rovnomerne rozložené celé čísla . Na nej je položená otáčavá drevená kružnica, na ktorej sú
opäť
rovnomerne rozložené celé čísla  v tomto poradí. Súčet týchto v tomto poradí. Súčet týchto
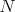 čísel je 1. Drevenú kružnicu vieme otočiť do čísel je 1. Drevenú kružnicu vieme otočiť do 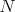 rôznych polôh tak, aby
čísla na nej boli umiestnené práve nad číslami kovovej
kružnice. Pre danú polohu
drevenej kružnice urobíme súčet rôznych polôh tak, aby
čísla na nej boli umiestnené práve nad číslami kovovej
kružnice. Pre danú polohu
drevenej kružnice urobíme súčet 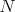 súčinov takých, že vynásobíme číslo na
drevenej kružnici s číslom na kovovej kružnici, ktoré sa
nachádza pod ním. Keďže
rôznych polôh drevenej kružnice je súčinov takých, že vynásobíme číslo na
drevenej kružnici s číslom na kovovej kružnici, ktoré sa
nachádza pod ním. Keďže
rôznych polôh drevenej kružnice je 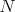 , tak aj týchto súčtov dostaneme , tak aj týchto súčtov dostaneme 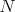 .
Ukážte, že všetky tieto súčty sú rôzne. .
Ukážte, že všetky tieto súčty sú rôzne. |



