Zadanie:
Marika a Meky hrajú hru. Marika ide prvá a napíše na tabuľu jedno
z čísel 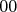 , , 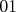 , , 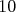 alebo alebo 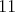 . V ďalších svojich ťahoch bude pridávať . V ďalších svojich ťahoch bude pridávať 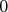 alebo alebo  na koniec doteraz napísaného čísla. Meky vo svojom ťahu vymení
medzi sebou ľubovoľné dve už napísané cifry. Hráči sa v
ťahoch striedajú. Hra končí, keď je na tabuli napísaných na koniec doteraz napísaného čísla. Meky vo svojom ťahu vymení
medzi sebou ľubovoľné dve už napísané cifry. Hráči sa v
ťahoch striedajú. Hra končí, keď je na tabuli napísaných 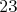 cifier a Meky urobil poslednú výmenu. Meky vyhrá vtedy, ak je
výsledné číslo symetrické (napríklad cifier a Meky urobil poslednú výmenu. Meky vyhrá vtedy, ak je
výsledné číslo symetrické (napríklad 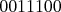 alebo alebo 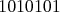 ). V opačnom prípade vyhrá Marika. Ktorý hráč vie vyhrať, aj
keď druhý hrá najlepšie ako môže (teda kto má víťaznú
stratégiu)? ). V opačnom prípade vyhrá Marika. Ktorý hráč vie vyhrať, aj
keď druhý hrá najlepšie ako môže (teda kto má víťaznú
stratégiu)? |



