kamilama - 12. 11. 2008 - 19:40:38 z 158.196.244.87.in-addr.arpamisko sz
napísal:
Rozmyslal som nad trosku jednoduchsim riesenim nez cez
KAGH. Najprv si rovnako ako misof vsimnime, ze 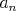 je vynimocne. Tak a teraz skusme dosadzovat. Pokus dosadit za vsetky
premenne 1 nevysiel. Skusim teda za je vynimocne. Tak a teraz skusme dosadzovat. Pokus dosadit za vsetky
premenne 1 nevysiel. Skusim teda za 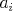 dostadit 1 a za dostadit 1 a za 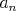 dostadit 2: dostadit 2:

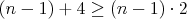
Tym som vylucil velke  a staci rozobrat tie male. a staci rozobrat tie male.
|
nj potialto som sa dostala aj ja...
cituj ma |
|
misko sz - 09. 11. 2008 - 10:25:32 z misko.kolej.mff.cuni.czRozmyslal som nad trosku jednoduchsim riesenim nez cez KAGH. Najprv si
rovnako ako misof vsimnime, ze 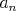 je vynimocne. Tak a teraz skusme dosadzovat. Pokus dosadit za vsetky
premenne 1 nevysiel. Skusim teda za je vynimocne. Tak a teraz skusme dosadzovat. Pokus dosadit za vsetky
premenne 1 nevysiel. Skusim teda za 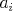 dostadit 1 a za dostadit 1 a za 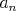 dostadit 2: dostadit 2:

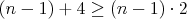
Tym som vylucil velke  a staci rozobrat tie male. Ale asi sa tym nevyhnem AG a tej
neprijemnej nesymetrii. Mimochodom, to misofove KA je skryte vo volbe
tych premennych. a staci rozobrat tie male. Ale asi sa tym nevyhnem AG a tej
neprijemnej nesymetrii. Mimochodom, to misofove KA je skryte vo volbe
tych premennych.
cituj ma |
|
Kubo - 08. 11. 2008 - 19:09:02 z adsl-dyn165.78-98-168.t-com.skAle riesit neznamena len riesit ale aj prestudovat vzorak ked som to
nevedel a vacsinou aj ked so vedel lebo tam mozu byt ina myslienky. cituj ma |
|
Nena - 08. 11. 2008 - 12:45:51 z adsl-dyn105.78-98-72.t-com.ska podľa mňa to nie je riešenie xD keď totiž začnem riešiť
gamu, budem jej rozumieť práve tak, ako 6b (akože vôbec), takže
akurát budem mať pocit, že gama je rovnako ťažká ako toto.. xD a
to, predpokladám, nie je pravda xD cituj ma |
|
Kubo - 07. 11. 2008 - 18:21:14 z adsl-dyn165.78-98-168.t-com.skpre vsetkych ktorym sa to zdalo tazke mam riesenie...snazte sa robit
gamu a bude sa vam toto zdat v pohode. cituj ma |
|
mišof - 05. 11. 2008 - 23:18:17 z adsl-dyn10.78-99-225.t-com.skNo hej, veď aj ja by som na strednej do tohto búšil hrubou silou a
snažil sa to nejak upravovať na štvorec a ono by to nejak vyšlo.
Len som chcel ukázať, že existuje aj elegantný postup :)
Ináč, celkom zaujímavá a jednoduchá možnosť (nie úplne
odlišná od tej prvej, len inak podaná) ešte môže ísť cez
nasledujúce pozorovanie:
Keď máme zvoliť  nezáporných čísel tak, aby ich súčet vyšiel nezáporných čísel tak, aby ich súčet vyšiel 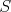 , tak súčet druhých mocnín zvolených čísel bude najmenší
vtedy, keď budú všetky rovnaké. , tak súčet druhých mocnín zvolených čísel bude najmenší
vtedy, keď budú všetky rovnaké.
Toto je pravda preto, že ak by dve z nich boli rôzne, nazvime ich  a a  , tak súčet ich druhých mocnín je , tak súčet ich druhých mocnín je  . Ak by sme ich obe nahradili číslom . Ak by sme ich obe nahradili číslom  , súčet tým nezmeníme a súčet druhých mocnín klesne na , súčet tým nezmeníme a súčet druhých mocnín klesne na 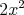 . .
No a pre túto úlohu z toho vyplýva: AK existuje nejaký
kontrapríklad, TAK existuje kontrapríklad, kde  . .
Tým sa zadanie mení na výrazne ľahšie 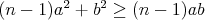 . . cituj ma |
|
škrečok - 05. 11. 2008 - 19:21:19 z 158.195.167.118HAgO napísal:
myslim, ze ako prvak by som to nezratal... |
a teraz už áno? :) btw. prváci v zime nemusia rátať šestku,
stačí sedmičku (aj to iba ak sú z matickej triedy, inak im stačí
1 až 5 :)).
cituj ma |
|
HAgO - 05. 11. 2008 - 18:50:17 z chello085216180252.chello.skmyslim, ze ako prvak by som to nezratal... cituj ma |
|
Baša <Pehavcek29~azet~sk> - 05. 11. 2008 - 16:58:39 z nat-1.aminet.skOMG... heh tento príklad asi nebudem mať ani za jeden bodík...
jejda nejako mi to nevyšlo... bol na alfu moc ťažký... :( cituj ma |
|
kamilama - 05. 11. 2008 - 16:26:10 z 158.196.244.87.in-addr.arpaa este chcem dodat ze som tretiacka ale co taki prvaci ktori ani
nevedia poratat kvadraticku rovnicu v tomto case este... a nemaju paru
o funkciach kvadratickych spojitych nespojitych definovanych atd...
myslim ze vazne je to moc tyc na alfu cituj ma |
|
kamilama - 05. 11. 2008 - 16:18:49 z 158.196.244.87.in-addr.arpahm ja len ze som tretiacka na obycajnom gympli a vzivote som sa
nestretla s inym ako aritmetickym priemerom a AG nerovnostou a
nesymetrickou nerovnostou takze asi bude neico zle.... hm no co uz
riesila som ako som vedela/nevedela a azda nejaky bodik dostanem cituj ma |
|
mišof - 05. 11. 2008 - 12:26:55 z adsl-dyn10.78-99-225.t-com.skJaj dokelu, ja chcem vedieť editovať príspevky, ešte aj ten
kvadratický priemer som napísal zle ja lama :P
Odmocnina má byť pochopiteľne druhá:
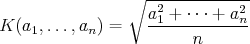
To je tak, keď rýchlo píšem a potom si to po sebe nečítam
poriadne. Hanba mi :P
cituj ma |
|
mišof - 05. 11. 2008 - 09:34:07 z adsl-dyn10.78-99-225.t-com.skA ešte všeobecnejšia verzia: Oni tie priemery tak ako sa klasicky
píšu vyzerajú strašne rozdielne, ale ono je to furt to isté.
Môžeme definovať priemer 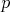 -teho stupňa tak, že umocníme každé číslo na -teho stupňa tak, že umocníme každé číslo na 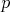 -tu, potom spravíme klasický (aritmetický) priemer, a výsledok
naspäť odmocníme. Teda -tu, potom spravíme klasický (aritmetický) priemer, a výsledok
naspäť odmocníme. Teda
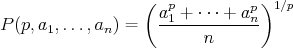
Pre  dostaneme aritmetický priemer, pre dostaneme aritmetický priemer, pre  kvadratický, pre kvadratický, pre 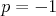 harmonický. harmonický.
Keď sa na to pozrieme ako na funkciu jednej premennej 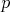 (teda akoby dosadíme ľubovoľné konkrétne (teda akoby dosadíme ľubovoľné konkrétne  ) tak zistíme, že pre ) tak zistíme, že pre  je to konštantná fcia a v ostatných prípadoch je vždy
rastúca. je to konštantná fcia a v ostatných prípadoch je vždy
rastúca.
(A síce tak, ako sme ju napísali, nie je definovaná v nule, ale je
spojitá, a dá sa ukázať, že keby sme ju v nule dodefinovali tak,
že nepokazíme spojitosť, bude P(0) práve geometrický
priemer.)
A z toho vyplývajú všetky nerovnosti medzi rôznymi priemermi.
Napríklad kubický priemer 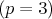 je vždy je vždy 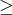 od harmonického od harmonického 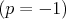 . .
Takto to vyzera pre  a a 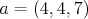 : http://people.ksp.sk/~misof/junk/priemery.png : http://people.ksp.sk/~misof/junk/priemery.png
(Hádajte k čomu ten graf konverguje pre 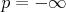 a a 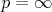 .) .)
cituj ma |
|
mišof - 05. 11. 2008 - 09:32:50 z adsl-dyn10.78-99-225.t-com.skJuj, v tom harmonickom mám bug, mi tam vypadlo  , ten má samozrejme byť , ten má samozrejme byť
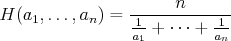
cituj ma |
|
mišof - 05. 11. 2008 - 09:12:18 z adsl-dyn10.78-99-225.t-com.skKeď máme  nezáporných čísel nezáporných čísel  , tak môžeme definovať veľa rôznych priemerov: , tak môžeme definovať veľa rôznych priemerov:
Normálny (aritmetický):
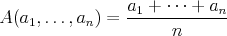
Geometrický:
![$ G(a_1,\dots,a_n) = \sqrt[n]{a_1\cdots a_n} $ $$ G(a_1,\dots,a_n) = \sqrt[n]{a_1\cdots a_n} $$](forum_tex/obr/tex/836.png)
Harmonický:
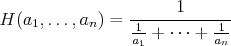
Kvadratický:
![$ K(a_1,\dots,a_n) = \sqrt[n]{ \frac{ a_1^2 + \cdots + a_n^2 }n } $ $$ K(a_1,\dots,a_n) = \sqrt[n]{ \frac{ a_1^2 + \cdots + a_n^2 }n } $$](forum_tex/obr/tex/839.png)
Klasický a brutálne často používaný fakt je AG-nerovnosť: vždy
platí  , pričom rovnosť nastáva len ak sú všetky , pričom rovnosť nastáva len ak sú všetky 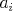 rovnaké. rovnaké.
Všeobecnejšia verzia je že vždy platí  , rovnosť tak isto. , rovnosť tak isto.
cituj ma |
|
skiller - 05. 11. 2008 - 08:19:46 z localhostmišof napísal:
No, prvý krok môjho riešenia som tu už napísal. Teraz sa na to
pozrieš ako na kvadratickú fciu premennej  . Keď chceme aby . Keď chceme aby 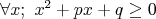 , tak musí platiť, že , tak musí platiť, že 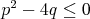 . V našom prípade to hovorí, že musí byť: . V našom prípade to hovorí, že musí byť:
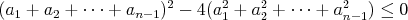
alebo po menšej úprave:
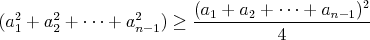
A to už podozrivo pripomína nerovnosť medzi aritmetickým a
kvadratickým priemerom, len je tam 4 namiesto  , takže zvyšok nechám na čitateľa :) , takže zvyšok nechám na čitateľa :)
|
Čo je nerovnosť medzi aritmetickým a kvadratickým priemerom? xD
cituj ma |
|
mišof - 05. 11. 2008 - 00:03:14 z adsl-dyn10.78-99-225.t-com.skNo, prvý krok môjho riešenia som tu už napísal. Teraz sa na to
pozrieš ako na kvadratickú fciu premennej  . Keď chceme aby . Keď chceme aby 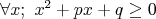 , tak musí platiť, že , tak musí platiť, že 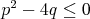 . V našom prípade to hovorí, že musí byť: . V našom prípade to hovorí, že musí byť:
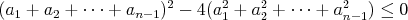
alebo po menšej úprave:
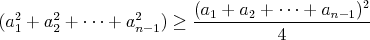
A to už podozrivo pripomína nerovnosť medzi aritmetickým a
kvadratickým priemerom, len je tam 4 namiesto  , takže zvyšok nechám na čitateľa :) , takže zvyšok nechám na čitateľa :)
cituj ma |
|
palo =) - 04. 11. 2008 - 22:11:27 z dial-92-52-9-250-orange.orange.skdalo sa to zratat aj nejako... pekne? teda, inak ako nechutnym busenim
do skaredych vyrazov s vela premennymi? cituj ma |
|
mišof - 04. 11. 2008 - 20:50:01 z adsl-dyn10.78-99-225.t-com.skEšte pridám hlbokú životnú múdrosť: Keď máme takúto
nesymetrickú nerovnosť, zväčša sa oplatí premenovať si tú zlú
neznámu, nech nám viac bije do očí:
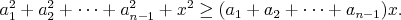
Tak, a hneď je tá úloha ľahšia, nie? :)
cituj ma |
|
mišof - 04. 11. 2008 - 20:25:26 z adsl-dyn10.78-99-225.t-com.skPod to sa aj ja podpíšem, tiež som si vravel, že takúto
asymetrickú nerovnosť dať do alfy je odvaha... ale zase, treba
tvrdo do vás, nech ste potom múdrejší :) cituj ma |
|
kamilama - 04. 11. 2008 - 19:52:13 z 158.196.244.87.in-addr.arpasom sama alebo sa to viacerym zdalo na sestku pritazke? cituj ma |
|



