Zadanie:
Na pol ceste do New Orleans sa Monty so Sinetuom zastavili na celý
deň v Brunchville, aby načerpali sily na druhú polovicu svojej
výpravy. Odviedli svoje kone do stajní a vybrali sa do
miestneho salónu. Zvesť o ich púti ich predbehla, a tak
na nich v salóne čakal obrovský jablkový koláč, ktorý im
upiekla manželka barmana. Keďže vedela, že Monty aj Sinetu
obľubujú matematiku, tak sa nedala zahanbiť a koláč
okorenila malou matematickou hádankou. Koláč mal tvar
rovnobežníka 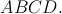 Stredy strán Stredy strán 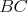 a a 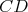 boli postupne ozdobené dvoma marcipánovými ružami boli postupne ozdobené dvoma marcipánovými ružami 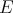 a a 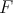 . Čokoládovou polevou boli vyznačené úsečky . Čokoládovou polevou boli vyznačené úsečky 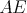 , , 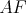 a a 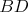 . Do priesečníku úsečiek . Do priesečníku úsečiek 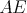 a a 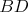 bola zabodnutá sviečka bola zabodnutá sviečka 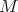 a do priesečníku úsečiek a do priesečníku úsečiek 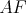 a a 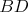 sviečka sviečka 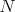 . Úlohou Montyho a Sinetua bolo dokázať, že sviečky delia
úsečku . Úlohou Montyho a Sinetua bolo dokázať, že sviečky delia
úsečku 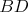 na tretiny, t.j., že platí na tretiny, t.j., že platí 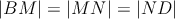 . Presvedčte sa, že dokážete rozmýšľať, aj keď myslíte na
koláč, a dokážte to tiež. . Presvedčte sa, že dokážete rozmýšľať, aj keď myslíte na
koláč, a dokážte to tiež.
|



