9. príklad 3. letnej série 2008/2009
Zadanie:
Nech  je nezáporné celé číslo. Dokážte, že číslo je nezáporné celé číslo. Dokážte, že číslo 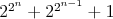 má aspoň má aspoň  rôznych prvočíselných deliteľov. rôznych prvočíselných deliteľov. |
kamilama - 12. 05. 2009 - 15:00:50 z 158.196.244.87.in-addr.arpanajlepsie 47 cituj ma |
|
beren - 11. 05. 2009 - 12:51:25 z adsl.wing.sk13 bodov by potesilo aj mna... cituj ma |
|
HAgO - 10. 05. 2009 - 21:21:06 z chello085216147110.chello.skchcem prvocislo bodov...dakujem... cituj ma |
|



