Zadanie:
Marek našiel doma gramofónovú platňu, na ktorej je napísaná
dvojica prirodzených čísel 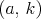 . Keď sa táto platňa dostane do blízkosti všetkých prirodzených
čísel, tak im začne skákať po hlavách. Najprv skočí na číslo . Keď sa táto platňa dostane do blízkosti všetkých prirodzených
čísel, tak im začne skákať po hlavách. Najprv skočí na číslo
 . Následne, keď sa nachádza na nejakom prirodzenom čísle . Následne, keď sa nachádza na nejakom prirodzenom čísle  ,1 tak sa správa podľa pravidiel: ,1 tak sa správa podľa pravidiel:
i) Ak je  deliteľné piatimi, preskočí na deliteľné piatimi, preskočí na 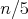 . .
ii) Ak  nie je deliteľné piatimi, preskočí na nie je deliteľné piatimi, preskočí na  . .
Takto sa to opakuje a platňa si skáče. Gramofónovú platňu
nazveme pokazenou, ak po istom čase začne dokola skákať
po tej istej sekvencii čísel. Pre aké dvojice prirodzených čísel
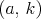 je Marekova platňa pokazená?%ako ma byt to druhe pokazena? je Marekova platňa pokazená?%ako ma byt to druhe pokazena?
1Najprv sa  rovná rovná  . . |



