|
|
 |
8. príklad 1. zimnej série 2009/2010
Zadanie:
Predstavte si, že okrem oviec má Chuck aj štvorčekovú mriežku
rozmerov 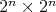 . Túto mriežku chce pokryť dlaždičkami. Každá dlaždička
pozostáva z troch štvorčekov a má tvar písmena L. Dlaždičky
môžu byť ľubovoľne otočené. Chuck má pre vás dve
úlohy: . Túto mriežku chce pokryť dlaždičkami. Každá dlaždička
pozostáva z troch štvorčekov a má tvar písmena L. Dlaždičky
môžu byť ľubovoľne otočené. Chuck má pre vás dve
úlohy:
a) Dokážte, že pre každé prirodzené číslo  môže Chuck vydlaždičkovať takúto mriežku, ak jej chýba jeden
rohový štvorček. môže Chuck vydlaždičkovať takúto mriežku, ak jej chýba jeden
rohový štvorček.
b) Nech 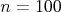 a v mriežke chýba jeden ľubovoľný štvorček. Rozhodnite, či
môže Chuck vždy vydlaždičkovať takúto mriežku. a v mriežke chýba jeden ľubovoľný štvorček. Rozhodnite, či
môže Chuck vždy vydlaždičkovať takúto mriežku. |
Syseľ - 13. 10. 2009 - 16:51:32 z gw-sa3.salamon.skSúhlasím z kamilamou cituj ma |
| kamilama - 13. 10. 2009 - 11:50:32 z edunet-static-169.87-197-28.telecom.skkvoli tomuto prikladu specialne je mi luto ze sa mi nedopatrenim
nepodarilo poslat KMS. Na veducovskej izbe UFO bol bordel, stratila
som obalku s rieseniami. Dalsi seriu uz isto poslem...
Ale tento priklad bol fakt super. cituj ma |
| |
| Petržlen <petrzlen~kms~sk> - 10. 10. 2009 - 22:52:10 z adsl-dyn115.78-99-72.t-com.skRozhodne pekný, hlavne keď a) tak krásne napomáha ku b)
Vlastne Ti stačí prípad  a potom konštrukcia prípadu a potom konštrukcia prípadu  cituj ma |
| HAgO - 10. 10. 2009 - 17:43:55 z chello089173090120.chello.sktento priklad sa mi páčil... cituj ma |
|
|
 |
|
|



