|
|
 |
7. príklad 1. zimnej série 2009/2010
Zadanie:
Austrálsky pastier Chuck sa po večeroch hráva so svojim
pravidelným 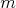 -uholníkom ( -uholníkom (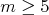 ). Každý vrchol ofarbí jednou zo šiestich farieb tak, aby medzi
jeho žiadnymi piatimi po sebe idúcimi vrcholmi neexistovali vrcholy
ofarbené rovnakou farbou. Zistite hodnoty, ktoré môže nadobudnúť ). Každý vrchol ofarbí jednou zo šiestich farieb tak, aby medzi
jeho žiadnymi piatimi po sebe idúcimi vrcholmi neexistovali vrcholy
ofarbené rovnakou farbou. Zistite hodnoty, ktoré môže nadobudnúť
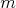 . . |
mišof - 11. 10. 2009 - 21:43:48 z dial-95-105-152-199-orange.orange.skevita: Ten zápis čo použil 4ndrejm hovorí: riešenia sú všetky
prirodzené čísla, ktoré sa dajú poskladať ako súčet
niekoľkých (možno aj 0) pätiek a niekoľkých (možno aj nula)
šestiek. Tento zápis v podstate zodpovedá jednej možnosti ako
zostrojiť riešenie: napr. keď máš 16 vrcholov, tak 16=5+5+6, a
tomuto zodpovedá ofarbenie (1,2,3,4,5, 1,2,3,4,5, 1,2,3,4,5,6).
Ešte stále treba dokázať to, že pre žiadne z ostatných čísel
sa to nedá, ale už aspoň vieš povedať, že pre tieto sa to dá a
tiež prečo sa to pre ne dá. cituj ma |
| evita <evita~branicka~gmail~com> - 11. 10. 2009 - 15:30:19 z adsl-dyn16.78-99-29.t-com.skhej ale ja by som hentakym zapisom nepochopila :DDD...nechapem, co
nahradzuje v tom vzorci k/k-1.... cituj ma |
| Petržlen <petrzlen~kms~sk> - 10. 10. 2009 - 22:44:45 z adsl-dyn115.78-99-72.t-com.skVýhody toho matematického výrazu sú:
a) vidíš, ako to funguje
b) je kratší a jednoznačnejší
c) núti Ťa to premýšľať, čo to vlastne znamená a preto tomu
lepšie pochopíš (a lepšie si to zapamätáš)
Vymenúvanie možností je také, že nie nutne vidíš súvislosti za
tým... cituj ma |
| ujo - 10. 10. 2009 - 16:05:41 z adsl-d31.84-47-21.t-com.skevita napísal:
ano je to pravda ale ked si to tak vezmete....5 a 6 to mozu byt... o
tom niet pochyb, potom tiez 10, 11 a 12; 15,16,17 a 18 a potom ale uz
od 20 to mozu byt hoc ake nie??? nebolo by teda spravnejsie zapisat to
ze mmoze byt v N väcsie alebo sa rovna 5 ale nemozu to byt cisla 7,
8, 9, 13, 14 a 19???? |
Áno, ale nie správnejšie, ale skôr jednoduchšie. :D
cituj ma |
| evita <evita~branicka~gmail~com> - 10. 10. 2009 - 14:33:44 z v02-15.opera-mini.netano je to pravda ale ked si to tak vezmete....5 a 6 to mozu byt... o
tom niet pochyb, potom tiez 10, 11 a 12; 15,16,17 a 18 a potom ale uz
od 20 to mozu byt hoc ake nie??? nebolo by teda spravnejsie zapisat to
ze mmoze byt v N väcsie alebo sa rovna 5 ale nemozu to byt cisla 7,
8, 9, 13, 14 a 19???? cituj ma |
| Syseľ - 07. 10. 2009 - 20:02:56 z gw-sa3.salamon.skPrestante s tou všeobecnosťou! Mne sa čísla 5 a 6 páčia :-) cituj ma |
| |
| 4ndrejm - 06. 10. 2009 - 22:59:34 z 92.245.198.107No vo vseobecnosti by malo platit, ze 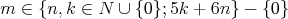 , imho... , imho... cituj ma |
| zas ten ujo - 06. 10. 2009 - 22:10:47 z adsl-dyn56.91-127-151.t-com.skpocul si? kamen mi spadol zo srdca :) cituj ma |
| bus - 06. 10. 2009 - 22:07:45 z dsl-static-251.213-160-168.telecom.skA tato odpoved je.... spravna! :) cituj ma |
| zvedavy ujo, ale nie uchyl <podskalka4ever~gmail~com> - 06. 10. 2009 - 21:15:12 z adsl-dyn56.91-127-151.t-com.skNeviem jak dlho uz tu su tieto diskusie, ale som rad ze som prvy, co
prispieva k 1. serii. som nedockavy, co sa tyka vysledkov, ale nie
poradie ale ake mali byt spravne riesenia :) neviem jakym zazrakom ale
mne v tomto priklade vyslo ze m nemôzu byt cisla 7,8,9,13,14,19. no
piste, pokarhajte ma, ze vam vyslo nieco ine. cituj ma |
|
|
 |
|
|



