9KzJcfi4 <fewmblsi4f~yahoo~com> - 28. 12. 2015 - 11:37:27 z 188.143.232.27Je9j, toto je pekne9 čedm som staršed, tfdm viac si uvedomujem,
že nie je df4ležite9 veľa toho stedhať, ale robiť tie spre1vne
veci. Prihove1ram sa za Slobodnfa školu :) cituj ma |
|
d6hsMux5p <isalsy80~gmail~com> - 26. 12. 2015 - 16:12:05 z 221.178.182.79Your cards are SO beautiful, and we would just LOVE to have you stop
by and share your cards with us in our cahrlengls at Word Art
Wednesday. Our challenges are never as fun without all our friends.
We care about you, hope you're doing well, and really hope to see you
playing along again soon with us at Word Art Wednesday.Be
blessed,Karen LWord Art Wednesdaywww.wordartwednesday.blogspot.com cituj ma |
|
d20JcPXVo5 <pnszql3emn4~gmail~com> - 26. 12. 2015 - 14:52:13 z 190-206-214-77.dyn.dsl.cantv.netDobrfd deň p. Machacek, do 10.4.2013 Ze1konnfd ze1stupca žiaka
pode1va prihle1šku riaditeľovi ZŠ. do 20.4.2013 Riaditeľ zašle
prihle1šky žiakov na SŠ vre1tane orsemočnfdch gymne1zied.S pozdrom
br. Peter Mage1č cituj ma |
|
|
|
yjCyQD5fi <vnorzvsamwg~mail~com> - 26. 12. 2015 - 13:51:42 z 188.143.234.155You actually did know your gdmnraa Challies. She died when Grace was
just two weeks old, so you would have been three at the time.Rick's
gdmnraa lokks so proud holding her great-granddaughter.Dad cituj ma |
|
Br4703EqSqM <i22uofqnx82~mail~com> - 27. 06. 2014 - 00:49:52 z 211.152.50.70[na 50% SPAM!]
Wow, superb blog luayot! How long have you
been blogging for? you made blogging look easy. The overall look of
your web site is excellent, as well as the content!. Thanks For Your
article about c4Œeknito Blog - Novc3bd dizajn . cituj ma |
|
fnra6OdY <9q081hf9ql~yahoo~com> - 26. 06. 2014 - 23:19:03 z 62-210-78-179.rev.poneytelecom.euS potěšenedm jsem si přečetl čle1nek o oceněned Dr.Kleislove9,
neboť jsem měl to obrovske9 štěsted, že mě paned pookesrrfa
učila. Při te9to předležitosti bych si proto dovolil doporučit
Vašed Asociaci absolventů GOH, abyste doporučili paned profesorku
na nominaci našemu vedened města na Cenu města Olomouce pro
předšted rok (letošned fadedlened cen jea0již rozhodnuto a
proběhne 14.6.2012). Jsem naprosto přesvědčen, že by si toto
oceněned zasloužila nejenom za svou odbornost a profesionalitu, ale
i za svou lidskost, neboť jsem měl tu čest poznat paned
profesorkua0po studiedch i osobně a jsem moca0re1d, že se s ned mohu
stfdkat dodnes.Roman Zelenka cituj ma |
|
6Apduslj <qzbszbjg~hotmail~com> - 26. 06. 2014 - 16:16:12 z 141.189.204.151. bukannya saya malas blaejar bahasa inggris, tetapi saya kurang
menguasai pelajaran bahasa inggris, jadi saya kurang memahami atau
mengerti jika bapa memberikan tugas atau pr. Sebenarnya saya menyukai
pelajaran bahasa inggris, hanya kurang mengerti saja dan kadang-kadang
tidak tau artinya jika ada pr atau tugas.2. saya terus berusaha sebisa
saya untuk bisa dan mengerti bahasa inggris, saya juga ingin bisa
berbahasa inggris yg baik dan menguasai pelajaran bahasa inggris, yg
saya inginkan hanya suasana kelas yg nyaman dan releks yg tidak
terlalu serius dan tegang dalam blaejar supaya saya lebih mudah
memahami dan mengerti apa yg bapa sampaikan ketika blaejar, dan dalam
menjelaskan saya ingin bapa tidak berbahasa inggris semuanya dalam
menerangkan suatu pelajaran, karena jika bapa berbahasa inggris dalam
menjelaskan, saya tidak bisa mengerti dan memahami apa yg bapa
jelaskan atau sampaikan. cituj ma |
|
mato - 26. 05. 2010 - 16:12:54 z dial-92-52-43-6-orange.orange.skZaujmave je aj ze ten vysledok je presne stvrtina vsetkych
trojuholnikov pri 2n+2 priamkach. cituj ma |
|
Feráč - 24. 05. 2010 - 11:10:14 z clpc340.comlab.ox.ac.ukZaujimalo by ma, preco to vyjde prave sucet prvych  stvorcov. Vie mi to niekto pekne intuitivne vysvetlit? stvorcov. Vie mi to niekto pekne intuitivne vysvetlit? cituj ma |
|
Fillippo - 23. 05. 2010 - 22:12:13 z ppp-77-234-226-61.dsidata.sktakisto, som dosiel po trik, ale dalej... pekna uloha. pacia sa mio
ulohy prepajajuce rozne oblasti matematiky cituj ma |
|
mato - 23. 05. 2010 - 19:45:02 z dial-92-52-43-6-orange.orange.skpo trik som sa dostal, ale trik ma uz nenapadol.. cituj ma |
|
Feráč - 23. 05. 2010 - 17:49:54 z worc-student-nat.worc.ox.ac.ukAby vám nebolo ľúto, že nie sú vzoráky, tak tu máte aspoň
veľmi stručné návody/riešenia.
Každej priamke vieme jednoznačne priradiť uhol z intervalu 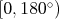 , ktorý zviera s x-ovou osou. Tri priamky s uhlami , ktorý zviera s x-ovou osou. Tri priamky s uhlami 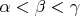 teraz tvoria ostrouhlý trojuholník práve vtedy, keď teraz tvoria ostrouhlý trojuholník práve vtedy, keď
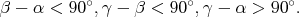
Úlohu si môžeme preformululovať: potrebujeme rozmiestniť 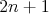 bodov do intervalu bodov do intervalu 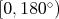 tak, aby tam bolo čo najviac takýchto trojíc tak, aby tam bolo čo najviac takýchto trojíc 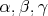 . .
Každá taká trojica má  a a 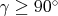 . Kde môže byť . Kde môže byť 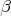 ? Buď ? Buď  a potom už stačí aby a potom už stačí aby 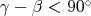 (prvý prípad), alebo (prvý prípad), alebo 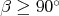 a potom už stačí aby a potom už stačí aby 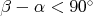 (druhý prípad). (druhý prípad).
Teraz trik. Nakreslime si všetky tieto body len do intervalu 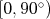 nasledovne. Body, ktoré sú nasledovne. Body, ktoré sú 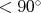 necháme na mieste a dáme im bielu (B) farbu. Body, ktoré sú necháme na mieste a dáme im bielu (B) farbu. Body, ktoré sú 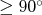 zmenšíme o zmenšíme o 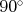 ("posunieme doľava") a nakreslíme ich čiernou (Č)
farbou. Žiadne dve priamky nie sú na seba kolmé, takže žiadne dva
body takto nepadnú na to isté miesto. Dobré trojice ("posunieme doľava") a nakreslíme ich čiernou (Č)
farbou. Žiadne dve priamky nie sú na seba kolmé, takže žiadne dva
body takto nepadnú na to isté miesto. Dobré trojice 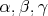 teraz presne zodpovedajú postupnostiam BČB (prvý prípad) a ČBČ
(druhý prípad). teraz presne zodpovedajú postupnostiam BČB (prvý prípad) a ČBČ
(druhý prípad).
Znovu si môžeme úlohu preformulovať: potrebujeme ofarbiť 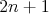 guľôčok čiernou a bielou farbou, aby sme dosiahli čo najviac
trojíc BČB a ČBČ (nie nutne susedných gúľočok). Toto je už
čisto kombinatorická úloha. Dokážte si, že najlepšie je dať
čierne a biele na striedačku. Potom to vyjde guľôčok čiernou a bielou farbou, aby sme dosiahli čo najviac
trojíc BČB a ČBČ (nie nutne susedných gúľočok). Toto je už
čisto kombinatorická úloha. Dokážte si, že najlepšie je dať
čierne a biele na striedačku. Potom to vyjde 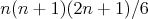 , presne tak ako vraví Mišof :) , presne tak ako vraví Mišof :)
cituj ma |
|
mišof - 22. 05. 2010 - 01:28:42 z dial-95-105-152-199-orange.orange.skAk sa nemýlim, tak odpoveď je 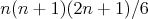 . . cituj ma |
|
Fillippo - 19. 05. 2010 - 22:39:42 z ppp-77-234-226-61.dsidata.skvie dakto aspon nejake hinty, alebo riesenie? celkom rad by som sa
niekde po troch tyzdnoch v tom priklade posunul. cituj ma |
|



