|
|
 |
7. príklad 1. zimnej série 2012/2013
Zadanie:
Cédečko má fóbiu z reálnych čísel  , , 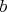 , ,  , ,  , , 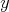 . Jeho strach je spôsobený tým, že platí . Jeho strach je spôsobený tým, že platí 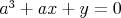 , , 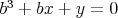 , , 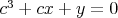 a navyše sú čísla a navyše sú čísla  , , 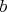 , ,  rôzne. Upokojí sa, iba ak sa dozvie, že súčet čísel rôzne. Upokojí sa, iba ak sa dozvie, že súčet čísel  , , 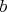 , ,  je nula. Dokážte, že sa nemá čoho báť. je nula. Dokážte, že sa nemá čoho báť. |
peťo <peto~kms~sk> - 10. 10. 2012 - 12:42:03 z 158.195.27.37škrečok
napísal:
no kebyže som ešte riešiteľ, tak toto by bolo moje
najkratšie riešenie ever...
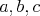 sú tri rôzne (a tým pádom všetky) korene kubickej rovnice sú tri rôzne (a tým pádom všetky) korene kubickej rovnice 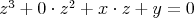 . potom z Vietovych vzťahov pre koeficient pri . potom z Vietovych vzťahov pre koeficient pri 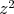 dostávame, že dostávame, že  , čo sme chceli dokázať. , čo sme chceli dokázať.
koľko mám bodov??? |
No, ak by si sa podpisal ako Zoltan Zvysz, tak by to asi bolo za 0,
lebo si nedokazal Vietove vztahy a nevysvetlil, co je to kubicka
rovnica a v ktorej premennej je to kubicke, a okrem toho, z Vietovych
vztahov mas 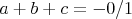 , takze to este musis upravit a nie napisat hned vysledok :). , takze to este musis upravit a nie napisat hned vysledok :).
cituj ma |
| |
|
|
 |
|
|



