|
|
 |
11. príklad 3. zimnej série 2008/2009
Zadanie:
V Žáboviciach sa uskutočnil turnaj, ktorého sa zúčastnilo  hráčov. Každý hral s každým práve jeden zápas v žábošachu,
pričom zápas vždy skončil výhrou jedného z hráčov. Dokážte,
že nech turnaj dopadol akokoľvek, vždy musí nastať jeden z dvoch
nasledujúcich prípadov. Buď môžme hráčov rozdeliť do dvoch
neprázdnych skupín hráčov. Každý hral s každým práve jeden zápas v žábošachu,
pričom zápas vždy skončil výhrou jedného z hráčov. Dokážte,
že nech turnaj dopadol akokoľvek, vždy musí nastať jeden z dvoch
nasledujúcich prípadov. Buď môžme hráčov rozdeliť do dvoch
neprázdnych skupín 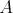 , , 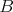 tak, že každý hráč z tak, že každý hráč z 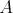 vyhral nad každým hráčom z vyhral nad každým hráčom z 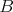 alebo vieme hráčov označiť alebo vieme hráčov označiť 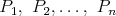 tak, že tak, že 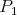 vyhral nad vyhral nad 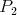 , , 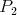 vyhral nad vyhral nad 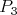 , ,  , , 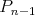 vyhral nad vyhral nad 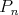 , , 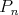 vyhral na vyhral na 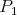 . . |
Bus - 07. 12. 2008 - 03:42:41 z dsl-static-251.213-160-168.telecom.skTo by si sa divil ktore vsetky priklady sa daju riesit bez papiera :).
Skus si aj take co sa ti zdaju ze by bez papiera nesli, pocvicis si
pamat a predstavivost. Mne sa tiez celkom pacil tym ze na neho netreba
mat ziadne vedomosti a da sa o nom premyslat hocikedy. A
pravdupovediac bolo v nom ovela menej moznosti na trapne chyby ako v
predchadzajucich jedenastkach. Takze tentokrat by si to uz mohol mat
mozno aj dobre :). (Ale riesenie som uz zabudol takze neviem ci bolo
tiez indukciou :(.) cituj ma |
| Kubo - 06. 12. 2008 - 17:52:56 z adsl-dyn158.78-98-36.t-com.skA skoda ja som myslel ze sa na mojej hrozne napisanej 11tke nastves aj
treti krat...:) ale mne sa celkom pacila dala sa riesit bez papiera.
Take ulohy sa mi pacia bo tie druhe sa mi menej chce robit. Dokonca si
myslim ze som to spravil dobre ale zase ked som to pisal na poslednu
chvilu asi neni ten popis dokonaly... a inac robil som to indukciou cituj ma |
| Bus - 06. 12. 2008 - 14:48:13 z dsl-static-251.213-160-168.telecom.skTak ako, dalo sa? Tentokrat to nebudem opravovat ja takze neviem aki
ste boli uspesni ale citim sa trochu zodpovedny za to ze tento priklad
presiel do zadani, takze komentujte :). cituj ma |
|
|
 |
|
|



