|
|
 |
11. príklad 3. zimnej série 2008/2009
Zadanie:
V Žáboviciach sa uskutočnil turnaj, ktorého sa zúčastnilo  hráčov. Každý hral s každým práve jeden zápas v žábošachu,
pričom zápas vždy skončil výhrou jedného z hráčov. Dokážte,
že nech turnaj dopadol akokoľvek, vždy musí nastať jeden z dvoch
nasledujúcich prípadov. Buď môžme hráčov rozdeliť do dvoch
neprázdnych skupín hráčov. Každý hral s každým práve jeden zápas v žábošachu,
pričom zápas vždy skončil výhrou jedného z hráčov. Dokážte,
že nech turnaj dopadol akokoľvek, vždy musí nastať jeden z dvoch
nasledujúcich prípadov. Buď môžme hráčov rozdeliť do dvoch
neprázdnych skupín 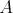 , , 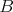 tak, že každý hráč z tak, že každý hráč z 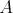 vyhral nad každým hráčom z vyhral nad každým hráčom z 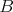 alebo vieme hráčov označiť alebo vieme hráčov označiť 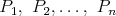 tak, že tak, že 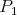 vyhral nad vyhral nad 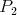 , , 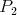 vyhral nad vyhral nad 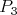 , ,  , , 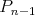 vyhral nad vyhral nad 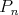 , , 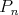 vyhral na vyhral na 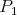 . . |
|
 |
|
|



