|
|
 |
10. príklad 3. letnej série 2007/2008
Zadanie:
Máme množinu desiatich rôznych reálnych čísel takú, že pre
každé dva jej rôzne prvky je ich súčin alebo ich súčet
racionálne číslo. Dokážte, že druhá mocnina každého čísla z
našej množiny je racionálne číslo. |
Jardo - 14. 05. 2008 - 13:30:53 z kms.skBody za túto úlohu sú už nejaký čas nahodené a nie sú tu
žiadne sťažnosti, tak usudzujem, že za ňu (skoro) každý dostal
očakávaný počet bodov.
Ukázalo sa však, že väčšina z Vás má nejasné, ba až mylné
predstavy o iracionálnych číslach. Vyskytli sa snahy vyjadrovať
reálne čísla v tvare "racionálna časť + iracionálna
časť", dokonca aj u skúsenejších riešiteľov. Pri takom
postupe ma napadajú hneď tri problémy:
1)Zadefinovanie: Čo to vlastne je (i)racionálna časť?
2)Jednoznačnosť: Dá sa každé číslo napísať jediným
spôsobom? Ak nie, nebude to problém?
3)Využiteľnosť: Čo tým skutočne získame?
Nikto zo spomínaných nevysvetlil ani prvý problém, zrejme preto,
že bolo cítiť nezrovnalosti. Takýto intuitívny prístup zdanlivo
funguje pre iracionálne čísla typu "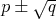 ". Dá sa ale pomerne ľahko dokázať, že číslo je
iracionálne, práve keď sa cifry jeho desatinného rozvoja nikdy
nezačnú cyklicky opakovať. Preto je iracionálne napríklad aj ". Dá sa ale pomerne ľahko dokázať, že číslo je
iracionálne, práve keď sa cifry jeho desatinného rozvoja nikdy
nezačnú cyklicky opakovať. Preto je iracionálne napríklad aj 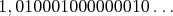 . .
Ako by Popoluška oddelila v takom čísle racionálnu a iracionálnu
zložku?? cituj ma |
| Jardo - 06. 05. 2008 - 19:02:55 z kms.skÚloha sa Vám zdala škaredá a podľa toho aj vyzerali riešenia.
Pritom v príklade sme toho vedeli pomerne veľa, takže sa dal
riešiť mnohými postupmi. Uvedieme dva prehľadné. Prvý ľahší
funguje pre aspoň sedem čísel, druhý trochu zložitejší pre
aspoň šesť. To je najlepší možný výsledok, lebo množina 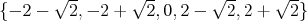 spĺňa podmienku, ale nie všetky jej prvky majú racionálny
štvorec. Pre prehľadnosť spojme červenou čísla s racionálnym
súčinom a zvyšné s racionálnym súčtom modrou. spĺňa podmienku, ale nie všetky jej prvky majú racionálny
štvorec. Pre prehľadnosť spojme červenou čísla s racionálnym
súčinom a zvyšné s racionálnym súčtom modrou.
Množina  má vlastnosť, že sčítaním, odčítaním, násobením a
nenulovým delením racionálnych čísel dostávame zasa racionálne
čísla (takzvaná uzavretosť množiny má vlastnosť, že sčítaním, odčítaním, násobením a
nenulovým delením racionálnych čísel dostávame zasa racionálne
čísla (takzvaná uzavretosť množiny 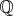 vzhľadom na tieto operácie). vzhľadom na tieto operácie).
Preto v modrom trojuholníku všetky čísla musia byť racionálne.
Ak 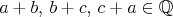 , ,
máme ![0,5\cdot [(a+b)-(b+c)+(c+a)]=a\in\Bbb Q $0,5\cdot [(a+b)-(b+c)+(c+a)]=a\in\Bbb Q$](forum_tex/obr/tex/631.png) . Podobne . Podobne 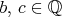 . .
V červenom trojuholníku bez núl musia byť racionálne aspoň
štvorce čísel.
Keďže 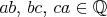 , tak , tak 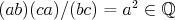 , podobne , podobne 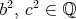 . .
R1 (inšpirované Vašimi riešeniami): Máme aspoň sedem čísel.
Vyberme ľubovoľné číslo  a ukážme, že jeho štvorec je racionálny (alebo dokonca samotné a ukážme, že jeho štvorec je racionálny (alebo dokonca samotné  ). Aspoň päť zvyšných čísel je nenulových. Máme dve
možnosti: ). Aspoň päť zvyšných čísel je nenulových. Máme dve
možnosti:
a) Z  vedú aspoň tri červené čiary (čiary vedú aspoň tri červené čiary (čiary 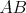 , , 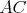 , , 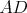 ). Ak je čiara ). Ak je čiara 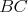 , , 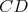 alebo alebo 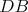 červená, máme červený trojuholník a červená, máme červený trojuholník a 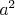 je racionálne. Inak máme modrý trojuholník je racionálne. Inak máme modrý trojuholník  a a 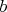 je racionálne. Potom aj je racionálne. Potom aj  je racionálne. je racionálne.
b) Aspoň tri čiary z  sú modré (čiary sú modré (čiary 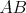 , , 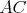 , , 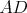 ). Ak je čiara ). Ak je čiara 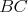 , , 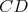 alebo alebo 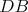 modrá, máme modrý trojuholník a modrá, máme modrý trojuholník a  je racionálne. Inak máme červený trojuholník je racionálne. Inak máme červený trojuholník  . Vtedy dostávame racionálne . Vtedy dostávame racionálne 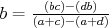 (delíme nenulovým číslom). Potom aj (delíme nenulovým číslom). Potom aj  je racionálne. Hotovo. je racionálne. Hotovo.
R2: Tento dôkaz používa teóriu grafov, ide to však aj bez nej.
Máme aspoň šesť čísel. Všímajme si päť nenulových. Máme tu
jednofarebnú kružnicu nepárnej dĺžky, inak by červený graf bol
bipartitný a bol podgrafom buď 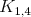 alebo alebo 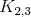 . Preto by modrý graf bol určite nadgrafom . Preto by modrý graf bol určite nadgrafom 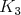 , spor. Na modrej kružnici sú čísla racionálne (sčítame súčty
na nepárnych miestach, odčítame tie na párnych a číslo, od
ktorého sme rátali, musí byť racionálne). Z uzavretosti , spor. Na modrej kružnici sú čísla racionálne (sčítame súčty
na nepárnych miestach, odčítame tie na párnych a číslo, od
ktorého sme rátali, musí byť racionálne). Z uzavretosti 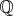 potom všetky čísla sú racionálne a tvrdenie platí. Na červenej
kružnici sú štvorce čísel racionálne (od určeného čísla
znásobíme súčiny na nepárnych miestach a vydelíme tými na
párnych) a to platí aj pre čísla pripojené červenou (ak je potom všetky čísla sú racionálne a tvrdenie platí. Na červenej
kružnici sú štvorce čísel racionálne (od určeného čísla
znásobíme súčiny na nepárnych miestach a vydelíme tými na
párnych) a to platí aj pre čísla pripojené červenou (ak je 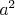 racionálne, aj racionálne, aj 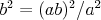 je racionálne). Majme číslo je racionálne). Majme číslo  pripojené len modrými čiarami, vezmime na kružnici tri po sebe
idúce čísla pripojené len modrými čiarami, vezmime na kružnici tri po sebe
idúce čísla  , , 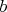 , ,  . Potom je racionálne . Potom je racionálne 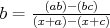 , a opäť sú všetky čísla racionálne. , a opäť sú všetky čísla racionálne. cituj ma |
|
|
 |
|
|



