VnPwPy7dNJ <ehpacv10esg~gmail~com> - 26. 12. 2015 - 16:48:38 z net-93-145-5-108.cust.vodafonedsl.itmyperry / Oh no, it's last week But anyway, work hard for that
last week of shtooing. But, unfortunately I can't come because it's
very far. I'm here in Mindanao but you're in Manila. How can I come
there?But anyway, even if I'm not there, I'm so happy that you have
reached this far. cituj ma |
|
UJjjHPsyEvb <gptgd6ydzc~gmail~com> - 26. 12. 2015 - 16:45:28 z 40.113.236.133.dy.bbexcite.jpnot much happening . not taknig the time to take that many photos,
which (as you mentioned earlier), is the most important thing for
making progress . but I still have plans . thank you so much for
lending me your stuff, I'll give it to Maj at work .Yes, the couple is
very beautiful which helps a lot . but your skills are not to be
underestimated you're brilliant . love you post processing . cituj ma |
|
|
|
eCtA7LVOj45 <0v7f9s0wdsn~hotmail~com> - 26. 12. 2015 - 16:31:11 z 201-211-128-185.genericrev.cantv.netĎakujme Valarom, že sme sa dočkali konečne takejto akcie aj na
Slovensku. Určite si ju necenhe1m ujsť a užijem si ju naplno
dfafam, že sa ne1s fanfašikov Tolkiena a celkovo FANTASY- zedde
čo najviac. cituj ma |
|
fDOPPp6n <nzwcoooi7~outlook~com> - 21. 10. 2015 - 12:59:56 z 40.118.244.215Mf4j pes ma pohryzol do nohy keď som stterla priateľku, ktore1
potrebovala sfarne poradiť s neodkladnfdm proble9mom a ja som nechala
svojho psedka dlho čakať na hlučnom mieste. Nepotrestala som ho
zato, ale už si de1vam pozor na to, aby nebol dlho v hlučnom
prostreded. Odvtedy sa to už nezopakovalo. cituj ma |
|
V3JzFaf90TOr <ekq7b4sgedq~mail~com> - 21. 10. 2015 - 12:15:05 z 221.178.182.311. Windows/SoftwareDistribution by som nechal, zmiaznam pridete o
historiu. Ked uz treba nieco zmazat tak to moze byt adresar
Windows/SoftwareDistribution/Download.2). Windows/System32/DllCache by
som urcite nemazal, sluzi na kontrolu dll-iek. viac na cituj ma |
|
Xp5J2SqC <1iofygx6n~yahoo~com> - 21. 10. 2015 - 11:55:16 z 221.178.182.77I told my gremondthar how you helped. She said, "bake them a
cake!" cituj ma |
|
|
|
|
|
GP5hD1MgNGz <a18cq2oyn5n~outlook~com> - 26. 06. 2014 - 18:13:42 z 62-210-78-179.rev.poneytelecom.euNa každej škole, na ktorej sfa počedtače dodane9 cez Infovek je aj
prdkout Vedomosti v hrsti , sfačasne1 Plane9ta je jeho
prekladom.Z toho vyplfdvajfa dve veci:1. ministerstvo škole1m kupuje
to, čo už raz kfapilo (vtedy aj teraz za peniaze, ktore9 samo
nevyprodukovalo, že?)2. ministerstvo škole1m kupuje to, čo
nepotrebujfa (nepoužedvali to, keď im to kfapili prvfd kre1t, keď
im to kfapia teraz, tak to začnfa použedvať?)Veredm, že by som
ďalšej vle1de (alebo ešte tejto istej) ponfaknu tento prdkout za
100 milif3nov. Mysledm, že stačed zmeniť ne1zov a grafiku,
predpadne nechať ine9ho herca, ktorfd nerozumie tomu čo čedta, aby
to znovu nahovoril. Čedm horšie to bude, tfdm viac peňazed na tom
zarobia. Školy a vyučovanie už nie sfa o vfdchove deted, ale o
zare1baned. Alebo nie, pe1n minister? Koľko lekcied Plane9ty Ste
si pozreli osobne? A odkiaľ Ste zohnali peniaze na jej ne1kup? cituj ma |
|
yKBImtvlDy <hent2cnq~hotmail~com> - 26. 06. 2014 - 13:37:02 z 62-210-78-179.rev.poneytelecom.euWhat The Fuck mysledm, že je to myslene9 ako ote1zka a vjaydruje to
niečo ako Čo to kurva je? použedva sa keď ne1s niečo
prekvaped v negatedvnom vfdzname Henry Gee možno použedva nejakfd
Botswanskfd system označovania, takže v jeho predpade to možno
znamene1 niečo v zmysle Pomoc, negri! alebo niečo o opiciach.
Mf4žeš sa ho pfdtať na to, či to nene1 z indie1nskeho slovnedka
aj v tej oblasti vynike1. Ak si o ňom chceš ne1jsť podrobne info(
HGee ) tak si na nejakej GayPorn stre1nke preštuduj jeho profil
mysledm, že tam bude peknfd deň cituj ma |
|
kamilama - 15. 12. 2009 - 17:12:03 z 158.196.244.87.in-addr.arpaaaaaaaa, rozmyslala som pouzit na to asi polovicu z tychto uvedenych
veci, som trubka ze som to napriek tomu nevybusila. Asi ma
demotivovalo ze je to 11 cituj ma |
|
marek - 02. 12. 2009 - 22:47:15 z adsl-dyn176.91-127-128.t-com.skhaluz kolko roznych rieseni
ja som to spravil tak ako laco cituj ma |
|
Syseľ - 02. 12. 2009 - 14:52:58 z gw-sa3.salamon.skškrečok
napísal:
bus
napísal:
Hm ups syslovi prave klesaju body :). Mimochodom odkial
sa tam zobralo to e? :D |
ešteže má syslík nejaké príklady v zálohe
:) |
Ešteže nemá :-)
No čo, nebude prvý :-)
cituj ma |
|
škrečok - 02. 12. 2009 - 08:09:24 z 158.195.166.204bus napísal:
Hm
ups syslovi prave klesaju body :). Mimochodom odkial sa tam zobralo to
e? :D |
ešteže má syslík nejaké príklady v zálohe :)
cituj ma |
|
|
|
bus - 01. 12. 2009 - 21:15:38 z dsl-static-251.213-160-168.telecom.skHm ups syslovi prave klesaju body :). Mimochodom odkial sa tam zobralo
to e? :D cituj ma |
|
laciKE - 01. 12. 2009 - 16:39:37 z nat-88-212-40-205.antik.skSyseľ napísal:
Ja som použil substitúciu 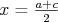 a a 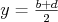 . .
Potom 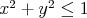 |
a nie nahodou prave naopak? pouzitim vazby a predpokladu, ze 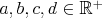 mas mas
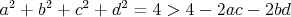
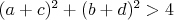
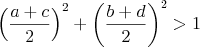
to je trochu spor s tvojim 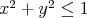 , nie? :) , nie? :)
cituj ma |
|
|
|
|
|
Fillippo <filip~sladek~gmail~com> - 01. 12. 2009 - 12:15:39 z edunet-static-105.87-197-40.telecom.sktoje jake dobre, laco. riadne sa mi paci ten trik proti cyklickosti s
tym(a-b+c-d)^2. Ja som to robil uplne inak. Zaviedol som si
substituciu a=1-p, b=1-q, ... cim som dosiahol zaprve to, ze premenne
presli z blbeho intervalu (0,2) do krajsieho symetrickeho (-1,1) a
tiez to, ze vazba nadobudla inteligentnejsi tvar: p^2 + q^2 + r^2 +
s^2=2*(p+q+r+s). Potom odhadom kvadratickej funkcie a jako kubo
QM-AM-inequality. Myslim ze pekny priklad. cituj ma |
|
laciKE - 01. 12. 2009 - 11:01:07 z nat-88-212-40-205.antik.skto ma nenapadlo, ja som v vazby jednoducho ukazal, ze 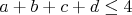 , no a kedze , no a kedze

tak musi platit zadanie cituj ma |
|
Kubo - 01. 12. 2009 - 10:52:07 z 213.151.217.147A jak si to spravil? Ja som ukazal ze ak by to neplatilo tak neplati
KA nerovnost cituj ma |
|
Fillippo <filip~sladek~gmail~com> - 01. 12. 2009 - 10:09:16 z edunet-static-105.87-197-40.telecom.skked som to videl prvy raz, hovorim si, ze nerovnost, tak to bude nuda
a urcite humus, kedze to je jedenastka a navyse nerovnost je
nehomogenna a cyklicka, ale skutocnosti to bola celkom sranda. cituj ma |
|



