Zadanie:
Monty presvedčil indiánov, aby sa hru hrali iba s 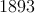 mincami, a tak sa už po chvíli mohol porozprávať so
Sinetuom. Podelil sa s ním o svoje zážitky
a vyložil mu, čo má v pláne. Sinetu ihneď súhlasil,
že mu pomôže a odbehol sa zbaliť. Monty išiel zatiaľ
pozrieť miestneho šamana. Ten si Montyho a jeho bystrú hlavu
už dávno obľúbil, a tak mu rovno zadal jeho najnovšiu
úlohu. Monty má dokázať, že pre každé prirodzené číslo mincami, a tak sa už po chvíli mohol porozprávať so
Sinetuom. Podelil sa s ním o svoje zážitky
a vyložil mu, čo má v pláne. Sinetu ihneď súhlasil,
že mu pomôže a odbehol sa zbaliť. Monty išiel zatiaľ
pozrieť miestneho šamana. Ten si Montyho a jeho bystrú hlavu
už dávno obľúbil, a tak mu rovno zadal jeho najnovšiu
úlohu. Monty má dokázať, že pre každé prirodzené číslo  , väčšie ako jedna, existuje , väčšie ako jedna, existuje  rôznych prirodzených čísel spĺňajúcich nasledovnú podmienku:
pre ľubovoľné dve čísla rôznych prirodzených čísel spĺňajúcich nasledovnú podmienku:
pre ľubovoľné dve čísla  , , 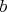 z tejto z tejto  -tice platí, že -tice platí, že  delí delí  . Nebuďte mrchožrúti a dokážte to aj vy. . Nebuďte mrchožrúti a dokážte to aj vy.
|



