Zadanie:
Nech 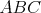 je trojuholník s opísanou kružnicou je trojuholník s opísanou kružnicou  a uhlami a uhlami 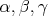 postupne pri vrcholoch postupne pri vrcholoch 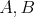 a a 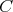 . Označme bod . Označme bod 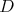 ležiaci v opačnej polrovine od bodu ležiaci v opačnej polrovine od bodu 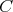 vzhľadom na priamku vzhľadom na priamku 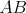 , pre ktorý , pre ktorý 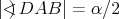 a a 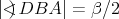 . Rovnakým spôsobom označíme body . Rovnakým spôsobom označíme body 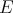 a a 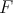 pre strany pre strany 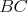 a a 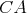 . Ukážte, že ak bodom . Ukážte, že ak bodom 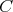 hýbeme po oblúku hýbeme po oblúku 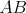 kružnice kružnice  (obsahujúcom bod (obsahujúcom bod 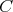 ), tak sa veľkosť uhla ), tak sa veľkosť uhla 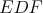 nemení. nemení. |



