Zadanie:
Nech 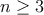 je prirodzené číslo. Žaba skáče pozdĺž číselnej osi.
Začína na čísle je prirodzené číslo. Žaba skáče pozdĺž číselnej osi.
Začína na čísle 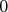 a urobí a urobí  skokov: Jeden dĺžky skokov: Jeden dĺžky  , jeden dĺžky , jeden dĺžky 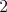 , ..., jeden dĺžky , ..., jeden dĺžky  . Tieto skoky môže urobiť v ľubovoľnom poradí. Ak však žaba
sedí na kladnom čísle, ďalší skok musí urobiť doľava (smerom
do záporných čísel) a ak je na nekladnom čísle, ďalší skok
musí urobiť doprava. Nájdite najväčšie prirodzené číslo . Tieto skoky môže urobiť v ľubovoľnom poradí. Ak však žaba
sedí na kladnom čísle, ďalší skok musí urobiť doľava (smerom
do záporných čísel) a ak je na nekladnom čísle, ďalší skok
musí urobiť doprava. Nájdite najväčšie prirodzené číslo  také, že žaba vie urobiť svojich také, že žaba vie urobiť svojich  skokov tak, aby nikdy nebola na žiadnom z čísel skokov tak, aby nikdy nebola na žiadnom z čísel 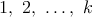 . .
|



