|
|
 |
14. príklad 1. letnej série 2008/2009
Zadanie:
Na zjazde matematikov sa stretlo 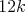 účastníkov a každý z nich sa pozdravil s práve účastníkov a každý z nich sa pozdravil s práve 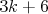 inými matematikmi. Pre každú dvojicu zúčastnených je počet
ľudí, ktorí pozdravili oboch, rovnaký. Koľko ľudí sa stretlo na
zjazde? (Pozdravovanie je symetrické.) Pre tento počet popíšte
prípad, kedy táto situácia nastáva. inými matematikmi. Pre každú dvojicu zúčastnených je počet
ľudí, ktorí pozdravili oboch, rovnaký. Koľko ľudí sa stretlo na
zjazde? (Pozdravovanie je symetrické.) Pre tento počet popíšte
prípad, kedy táto situácia nastáva. |
bus - 07. 03. 2009 - 23:18:21 z dsl-static-251.213-160-168.telecom.skHm. Fakt. Sa divim ze toto riesenie v tej algebraickej knizke nebolo.
:D Alebo som ho tam len cez tie pismenka nevidel. cituj ma |
| Kubo - 07. 03. 2009 - 09:40:10 z adsl-dyn50.78-98-16.t-com.skhej uz som pochopil... a tie vase znacky vyzeraju skor jak chemicke
prvky cituj ma |
| |
| misko sz - 07. 03. 2009 - 00:03:38 z misko.kolej.mff.cuni.czNo ked sa prekryvaju, vtedy budu mat 6 :)
Ale ondrac zahmlieva, tie priamky v 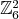 su take priamky-nepriamky... Proste body [x,y] tvaru ax+by=c, ked to
beries modulo 6. Asi. su take priamky-nepriamky... Proste body [x,y] tvaru ax+by=c, ked to
beries modulo 6. Asi. cituj ma |
| Kubo - 06. 03. 2009 - 22:25:28 z adsl-dyn50.78-98-16.t-com.skAko ma fungovat to ze 2 priamky maju 1 alebo 6 priesecnikov? cituj ma |
| Ondráč - 06. 03. 2009 - 17:34:54 z pupendo.ubyt.sdjls.uniba.skFajn :) Moje riešenie spočívalo v štvorci 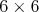 a každý bod susedí s troma priamkami, ktoré ním prechádzajú
(také diskrétne priamky). Potom sa tam veľmi pekne dá využiť to,
že dve priamky majú práve jeden, alebo 6 priesečníkov a výsledok
je na svete. Skúste si to už domyslieť sami :) (Aby sme s Busom
neprezradili každý detail ;)) a každý bod susedí s troma priamkami, ktoré ním prechádzajú
(také diskrétne priamky). Potom sa tam veľmi pekne dá využiť to,
že dve priamky majú práve jeden, alebo 6 priesečníkov a výsledok
je na svete. Skúste si to už domyslieť sami :) (Aby sme s Busom
neprezradili každý detail ;)) cituj ma |
| bus - 06. 03. 2009 - 16:40:20 z dsl-static-251.213-160-168.telecom.skLahsie sa to checkuje ked si to nakreslis. Ja som si to kreslil ako
styri poschodia stvorcov 3x3. Potrebujes dokazat, ze pre kazdy vektor
(ijk) existuje presne 6 usporiadanych dvojic bodov z mojej mnoziny
(oznacme ju M), ktore sa lisia o (ijk). Inac povedane, ak vezmes M a
jej kopiu posunutu o (ijk), musia mat tieto dve mnoziny vzdy presne
sestprvkovy prienik. Vyhodou M je to, ze pre lubovolne dve rozne
poschodia p a p+i plati, ze ked poschodie cislo p posunies o (ijk) tak
takto ziskana mnozina bude mat prienik s poschodim p+i nezavisly od j
a k. (Napriklad poschodie 0 ma s poschodim 1 vzdy 2-prvkovy prienik
atd.) cituj ma |
| Ondáč - 06. 03. 2009 - 07:34:13 z pupendo.ubyt.sdjls.uniba.skIdem teraz do skoly, takze to nestiham checkovat, ale Bus je nadejny
aspirant na margotku :) Moje riesenie ma tiez taku nejaku modulovu
strukturu :) Ale je len dvojrozmerne :) cituj ma |
| bus - 06. 03. 2009 - 01:00:54 z dsl-static-251.213-160-168.telecom.skOk tak toto je the best co sa mi zatial podarilo: Usporiadaj si
vrcholy do kvadra 4x3x3. Vrchol (000) bude susedit s vrcholmi:
(010), (011), (012), (020), (021), (022), (100), (110), (120), (200),
(211), (222), (300), (312), (321).
Vrchol (abc) potom bude susedit s tymi istymi vrcholmi ako (000) ale
posunutymi o vektor (abc). (Samozrejme modulo prislusne rozmery
kvadra.) cituj ma |
| bus - 05. 03. 2009 - 12:29:38 z dsl-static-251.213-160-168.telecom.skSom zvedavy :). Ze by som pozrel vzorak? cituj ma |
| Ondráč - 05. 03. 2009 - 10:41:40 z pupendo.ubyt.sdjls.uniba.skTento sa dá :) Však to bude na niekoľko riadkov vo vzoráku :) cituj ma |
| bus - 05. 03. 2009 - 03:03:20 z dsl-static-251.213-160-168.telecom.skAka nahodicka, presne toto teraz bereme na kombiantorike so Skovierom.
Ked sa chces nieco poducit Ondrac tak prid ;). Alebo googli
"Symmetric Balanced Incomplete Block Designs". Co treba je
SBIBD (36, 15, 6), skusal som to googlit a nasiel nejake skonstruovane
vo viacerych clankoch ale obavam sa ze ziadnym "jednoduchym"
sposobom sa asi nedaju predstavit :P. cituj ma |
| Ondráč - 04. 03. 2009 - 18:18:19 z pupendo.ubyt.sdjls.uniba.sk:) Fajn, takže už vieme, že taký graf existuje, ale margotka je
ešte nepridelená, čakám na nejaký elegantný popis takého grafu
:) cituj ma |
| katka - 04. 03. 2009 - 16:52:14 z 158.195.167.67Tak mne sa podarilo riesenie vygooglit (to ani nie je hruba sila, skor
sikovnost hladania :) ), ale za taketo riesenie si nezasluzim, a ani
nechcem margotku. Vdaka tomuto prikladu som sa dozvedela, co su silne
regularne grafy:
http://mathworld.wolfram.com/StronglyRegularGraph.html. No a riesenie
mozte nejst tu: http://www.maths.gla.ac.uk/~es/36.vertices, pohladajte
tam dim=36, degree=15, lambda=6, mu=6, zacina to asi tak v strede.
Vraj existuje az 227 takych neizomorfnych grafov. Zatial aj tak
neviem, ako vyzeraju tie grafy, lebo su tam len incidencne matice a
velmi sa mi nechce prekreslovat si to do obrazkov...
V kazdom pripade by ma zaujimala nejaka elegantna metoda, ako najst
taky graf. cituj ma |
| Ondráč - 04. 03. 2009 - 15:24:48 z pupendo.ubyt.sdjls.uniba.skViacerí ste dokázali, že musí platiť  a pre ľubovoľnú dvojicu matematikov existuje práve a pre ľubovoľnú dvojicu matematikov existuje práve 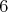 iných matematikov, s ktorými sa pozdravili. Nikomu sa však
nepodarilo taký prípad naozaj skonštruovať. Kto to zvládne ako
prvý, pred zverejnením vzoráku (alebo zhliadnutím), má u mňa
margotku (podľa vlastného výberu) :) Zúčastniť sa môže hocikto
(aj vedúci). Keďže víťaza posudzujem ja, tak odmietam riešenia
hrubou silou (počítačom nájdená správna konštelácia). Vaše
riešenia píšte sem. iných matematikov, s ktorými sa pozdravili. Nikomu sa však
nepodarilo taký prípad naozaj skonštruovať. Kto to zvládne ako
prvý, pred zverejnením vzoráku (alebo zhliadnutím), má u mňa
margotku (podľa vlastného výberu) :) Zúčastniť sa môže hocikto
(aj vedúci). Keďže víťaza posudzujem ja, tak odmietam riešenia
hrubou silou (počítačom nájdená správna konštelácia). Vaše
riešenia píšte sem. cituj ma |
|
|
 |
|
|



