Zadanie:
Centrum New Yorku sa skladá z  severojužných a severojužných a  západovýchodných ciest, ktoré tvoria štvorčekovú sieť \\ západovýchodných ciest, ktoré tvoria štvorčekovú sieť \\ 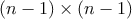 štvorcových blokov. V každej z štvorcových blokov. V každej z 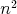 križovatiek sa nachádza autobusová zastávka. Po uliciach
premávajú autobusové linky so zastávkami vo všetkých
križovatkách. Trasa každej linky obsahuje najviac jednu zákrutu
a je obojsmerná. Koľko najmenej liniek je potrebných na to,
aby sa dalo medzi ľubovoľnými dvomi zastávkami cestovať na
najviac jeden prestup? Výsledok určte v závislosti od celého
čísla križovatiek sa nachádza autobusová zastávka. Po uliciach
premávajú autobusové linky so zastávkami vo všetkých
križovatkách. Trasa každej linky obsahuje najviac jednu zákrutu
a je obojsmerná. Koľko najmenej liniek je potrebných na to,
aby sa dalo medzi ľubovoľnými dvomi zastávkami cestovať na
najviac jeden prestup? Výsledok určte v závislosti od celého
čísla 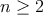 . Nezabudnite zdôvodniť, prečo menej liniek nestačí. . Nezabudnite zdôvodniť, prečo menej liniek nestačí.
|



