Zadanie:
Dané je reálne číslo  , ktoré je rôzne od , ktoré je rôzne od 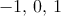 . Vodka a Hopko s ním hrajú nasledujúcu hru: Vo výraze . Vodka a Hopko s ním hrajú nasledujúcu hru: Vo výraze
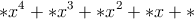
nahradzujú striedavo hviezdičky celočíselnými mocninami čísla  . Vodka začína. Na konci sa pozrú na to, či výsledný polynóm
má aspoň jeden reálny koreň. Ak áno, vyhráva Hopko, inak vyhrá
Vodka. Zistite v závislosti od . Vodka začína. Na konci sa pozrú na to, či výsledný polynóm
má aspoň jeden reálny koreň. Ak áno, vyhráva Hopko, inak vyhrá
Vodka. Zistite v závislosti od  , kto z nich má víťaznú stratégiu. , kto z nich má víťaznú stratégiu.
|



