Zadanie:
Šerifovi špehovia zistili, že na lúpeži sa podujme úplne celá
banda Drzohubých. Každý člen bandy má jedinečné identifikačné
číslo, ktoré je menšie ako 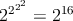 a v binárnom zápise neobsahuje ani trojicu za sebou
idúcich núl, ani trojicu za sebou idúcich jednotiek. (Číslo a v binárnom zápise neobsahuje ani trojicu za sebou
idúcich núl, ani trojicu za sebou idúcich jednotiek. (Číslo 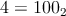 vyhovuje, ale číslo vyhovuje, ale číslo 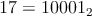 nemôže byť identifikačným číslom banditu, lebo
v binárnom zápise obsahuje trojčíslie nemôže byť identifikačným číslom banditu, lebo
v binárnom zápise obsahuje trojčíslie 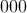 .) Navyše všetky povolené identifikačné čísla sú použité.
Monty so Sinetuom by radi vedeli, koľko banditov môžu očakávať.
Pomôžte im a zistite, koľko existuje rôznych
identifikačných čísel medzi .) Navyše všetky povolené identifikačné čísla sú použité.
Monty so Sinetuom by radi vedeli, koľko banditov môžu očakávať.
Pomôžte im a zistite, koľko existuje rôznych
identifikačných čísel medzi  a a 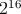 . .
|



