Zadanie:
Na tabuli je narysovaných 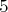 kružníc, kružníc, 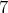 štvorcov a štvorcov a 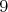 trojuholníkov, pričom žiadne dva z týchto útvarov nemajú
spoločný bod. Marek a Paľo sa hrajú hru, v ktorej striedavo robia
ťahy. Urobiť ťah znamená zotrieť ľubovoľné dva obrazce a
nahradiť ich jedným novým. Nový útvar sa na tabuľu nakreslí
tak, aby so žiadnym iným útvarom na tabuli nemal spoločný bod. V
jednom ťahu možno nahradiť trojuholníkov, pričom žiadne dva z týchto útvarov nemajú
spoločný bod. Marek a Paľo sa hrajú hru, v ktorej striedavo robia
ťahy. Urobiť ťah znamená zotrieť ľubovoľné dva obrazce a
nahradiť ich jedným novým. Nový útvar sa na tabuľu nakreslí
tak, aby so žiadnym iným útvarom na tabuli nemal spoločný bod. V
jednom ťahu možno nahradiť
- dve kružnice kružnicou,
- dva trojuholníky štvorcom,
- kružnicu a trojuholník trojuholníkom,
|
- dva štvorce trojuholníkom,
- kružnicu a štvorec štvorcom,
- štvorec a trojuholník kružnicou.
|
Paľo vyhrá, ak výsledkom bude štvorec. Marek vyhrá, ak na tabuli
zostane trojuholník. Ukážte, pre ktorého hráča existuje
víťazná stratégia, ak hru začína Marek. Popíšte túto
stratégiu.
Poznámka: Nájsť víťaznú stratégiu znamená popísať
postupnosť krokov, ktorá zaručí jednému z hráčov víťazstvo,
ak druhý hráč hrá úplne ľubovoľne. |



