|
|
 |
10. príklad 3. letnej série 2011/2012
Zadanie:
Kubo a Matúš zakopli o prirodzené číslo  , a tak sa rozhodli, že si zahrajú hru. V tejto hre budú striedavo
písať jednu z číslic , a tak sa rozhodli, že si zahrajú hru. V tejto hre budú striedavo
písať jednu z číslic 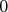 alebo alebo  na rolku toaleťáka. Každý napíše svoju číslicu hneď za
poslednú súperovu. Prehráva hráč, ktorý napíše číslicu, po
ktorej sa na toaleťáku objavia dve rovnaké na rolku toaleťáka. Každý napíše svoju číslicu hneď za
poslednú súperovu. Prehráva hráč, ktorý napíše číslicu, po
ktorej sa na toaleťáku objavia dve rovnaké  -tice za sebou idúcich číslic.1 Ukážte, že: -tice za sebou idúcich číslic.1 Ukážte, že:
a) Hra vždy skončí.
b) Ak začína Kubo a  je nepárne, tak Matúš dokáže vyhrať, aj keby Kubo hral
najlepšie ako dokáže. je nepárne, tak Matúš dokáže vyhrať, aj keby Kubo hral
najlepšie ako dokáže.
1Tieto  -tice sa môžu prekrývať, avšak nie v celej svojej dĺžke. -tice sa môžu prekrývať, avšak nie v celej svojej dĺžke. |
Terno - 14. 05. 2012 - 16:25:22 z 158.195.27.37Sôň napísal:
Správne hádam, že 2 body sa udeľovali za vyriešenie časti a) ?
:D (Za čo sa dával ten tretí, v prípade riešení za 3 body? :)
) |
Mozno za spravnu strategiu bez dokazu? :)
cituj ma |
| Sôň - 13. 05. 2012 - 18:00:06 z 114.ba.psg.skSprávne hádam, že 2 body sa udeľovali za vyriešenie časti a) ?
:D (Za čo sa dával ten tretí, v prípade riešení za 3 body? :) ) cituj ma |
|
|
 |
|
|



