Zadanie:
S tajným symbolom vo vrecku sa Monty vybral priamo
k táborisku Krivozubého Tonyho a niekoľkých ďalších
Drzohubých. Ukázal im papier so symbolom a ihneď ho vzali
medzi seba. Sedeli okolo švajčiarskej čokolády, ktorú nedávno
ulúpili a rozmýšľali, ako si ju rozdeliť. Čokoláda mala
tvar štvorca a tvorilo ju 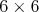 menších tabličiek. Chceli ju rozdeliť na deväť kúskov tak, aby
delili len pozdĺž tabličiek a aby im nič neostalo. Navyše
má mať každý z týchto kúskov tvar obdĺžnika (aj štvorec
je obdĺžnik). Banditi sa snažili rozdeliť čokoládu podľa
týchto pravidiel tak, aby bol každý kúsok iného
tvaru.1 Monty sa na chvíľku zamyslel, a potom
prehlásil, že to nie je možné. Vedeli by ste aj vy dokázať, že
sa vždy nájdu aspoň dva rovnaké kúsky? menších tabličiek. Chceli ju rozdeliť na deväť kúskov tak, aby
delili len pozdĺž tabličiek a aby im nič neostalo. Navyše
má mať každý z týchto kúskov tvar obdĺžnika (aj štvorec
je obdĺžnik). Banditi sa snažili rozdeliť čokoládu podľa
týchto pravidiel tak, aby bol každý kúsok iného
tvaru.1 Monty sa na chvíľku zamyslel, a potom
prehlásil, že to nie je možné. Vedeli by ste aj vy dokázať, že
sa vždy nájdu aspoň dva rovnaké kúsky?
1kúsky, ktoré sa líšia iba otočením, považujeme za
rovnaké |



