|
|
 |
8. príklad 2. letnej série 2007/2008
Zadanie:
Do tabuľky s veľkosťou 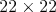 vpíšeme čísla vpíšeme čísla 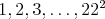 , každé práve raz. Je pravda, že vždy vieme vybrať dvojicu
políčok susediacich rohom alebo stranou tak, že súčet čísel
vpísaných v týchto políčkach bude deliteľný , každé práve raz. Je pravda, že vždy vieme vybrať dvojicu
políčok susediacich rohom alebo stranou tak, že súčet čísel
vpísaných v týchto políčkach bude deliteľný 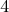 ? ? |
Jardo - 16. 04. 2008 - 14:27:40 z kms.skUhm, už len detail. Ako pozerám na vytlačené vzorové riešenie,
počas redikcie (?) došlo k chybičke v počte všetkých vyplnení
tabuľky zvyškami. Pre samotné riešenie je to takmer fuk, ale keby
sa to niekomu nezdalo, malo tam byť  . . cituj ma |
| |
| bus - 15. 04. 2008 - 15:08:15 z dsl-static-251.213-160-168.telecom.skTo je tak najviac deleno 8, a to tiež nie vždy. Stiahla si to asi
tak o jednu cifru :). cituj ma |
| Mustang - 13. 04. 2008 - 20:51:37 z static-081-022-141.dsl.nextra.skokej a aj tak to este musis vydelit istym poctom kedze nejake stredovo
ci osovo sumerne pripady neratam:o) cituj ma |
| misof - 11. 04. 2008 - 22:02:14 z spojar.lubbzonet.skMustang: Presne tak. Naozaj si to skús pre 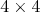 , už tam je tých možností dosť. Napríklad takáto: , už tam je tých možností dosť. Napríklad takáto:
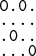
cituj ma |
| Mustang - 11. 04. 2008 - 21:52:30 z static-081-022-141.dsl.nextra.skok a to su vsetko pocty moznosti ulozenia nul takych, ze sa nedotykaju
ani rohmi? cituj ma |
| |
| bus - 10. 04. 2008 - 14:12:48 z dsl-static-251.213-160-168.telecom.skMyslím že mišof aj Justus rátajú tie nuly ako rovnaké, teda že
nezáleží na tom či vymeníš povedzme 4ku s 8kou. Aj tak je tých
možností veľa - skús si to pre 4x4. cituj ma |
| misof - 09. 04. 2008 - 22:03:43 z spojar.lubbzonet.skA pre 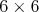 mi tých rozmiestnení vyšlo len 3600, nie 3616. mi tých rozmiestnení vyšlo len 3600, nie 3616. cituj ma |
| |
| Mustang - 09. 04. 2008 - 21:11:50 z static-081-022-141.dsl.nextra.skale ved to je nejaka somarina. ty tam ratas kazdu nulu (resp. dvojku)
ako inu? lebo inak nie je mozne aby tam bolo tolko roznych moznosti
ked to nemoze spolu susedit... uznavam ze ich je viac vyhovujucich,
ale tolko urcite nie... cituj ma |
| |
| katka j - 09. 04. 2008 - 14:07:17 z gjgt.skhm..ale ked uvazujem, ze tych cisel je 121 a nesmu spolu susedit, tak
je tych rozlozeni trosku menej, nie? cituj ma |
| Justus - 05. 04. 2008 - 17:53:44 z h3-21.nw.fmph.uniba.skPomerne veľa riešení bolo za 1b alebo za 9b, takú vysokú
disperziu som nečakal. Asi by sa hodilo poznamenať, že častou
chybou bol predpoklad, že vieme veľmi presne určiť rozloženie
čísel [0], resp. [2], v tabuľke. Niečo v tom zmysle, že je len
zopár možných uložení týchto čísel do tabuľky. To je ale
celkom mylné, počet tých možných rozložení je jedno veľmi
škaredé 60 -miestne číslo:( cituj ma |
| kamilama - 02. 04. 2008 - 16:55:09 z 158.196.244.87.in-addr.arpadobry priklad. ako zlozito som to najprv robila a potom vysvitlo ze je
to uplne lahke. ja vo vsetkom najprv hladam zakeraky a potom sa ukaze
ze ci to je zakerak alebo nie. toto nebol ta ho chvalim:) cituj ma |
| JeFo - 30. 03. 2008 - 14:45:33 z 214.125.119.217.in-addr.arpatak ja teda ako prvý pochválim.
dobrý príklad, dobrý príklad, len papkaj a neplac cituj ma |
| JeFo - 30. 03. 2008 - 14:44:45 z 214.125.119.217.in-addr.arpatak ja teda ako prvý pochválim.
dobrý príklad, dobrý príklad, len papkaj a neplac cituj ma |
| Justus - 29. 03. 2008 - 17:26:05 z h3-44.nw.fmph.uniba.skAko to, že tento pekný príklad ešte nikto nepochválil:( No tak
šup-šup do písania.
Pre ostatných tu máme riešenie. Oproti vzoráku sa bude trochu viac
venovať tomu, ako sme na tú-onú vec prišli.
R: V takejto úlohe potrebujeme najskôr pojať podozrenie, že to
buď ide alebo nejde. Preto si najskôr skúsme tabuľku nejako
premyslene vyplniť. Ako zjednodušovák nám poslúži poznatok, že
namiesto čísiel  , ,  , , 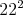 stačí používať ich zvyšky po vydelení štyrma, teda stačí používať ich zvyšky po vydelení štyrma, teda 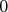 , ,  , , 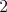 a a 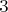 . Dvaja susedia tak budú mať súčet deliteľný štvorkou, práve
ak ho aj pôvodné čísla mali ňou deliteľný. Ukladajme čísla
tak, aby sme nemali taký súčet. Ak vyplníme celú tabuľku, tak
sme skončili. Ak sa nám to naopak nepodarí, tak by to mohlo niečo
znamenať. Snažíme sa teda izolovať jednotlivo nuly a dvojky a
nemiešať jednotky s trojkami. To by šlo napríklad tak, že
nepárne riadky vyplníme s . Dvaja susedia tak budú mať súčet deliteľný štvorkou, práve
ak ho aj pôvodné čísla mali ňou deliteľný. Ukladajme čísla
tak, aby sme nemali taký súčet. Ak vyplníme celú tabuľku, tak
sme skončili. Ak sa nám to naopak nepodarí, tak by to mohlo niečo
znamenať. Snažíme sa teda izolovať jednotlivo nuly a dvojky a
nemiešať jednotky s trojkami. To by šlo napríklad tak, že
nepárne riadky vyplníme s 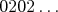 a párne riadky striedavo buď s a párne riadky striedavo buď s 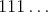 alebo alebo 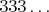 . Nepárnych riadkov je ale nepárny počet, takže by sme takto
nevpísali rovnaký počet jedničiek a trojiek. Ďaľšími drobnými
úpravami síce dôjdeme až k tabuľke s jedinkou dvojicou
nevhodných susedov, ktorých sa ale nie a nie zbaviť. To je už fakt
podozrivé. Všimnime si, že tabuľka . Nepárnych riadkov je ale nepárny počet, takže by sme takto
nevpísali rovnaký počet jedničiek a trojiek. Ďaľšími drobnými
úpravami síce dôjdeme až k tabuľke s jedinkou dvojicou
nevhodných susedov, ktorých sa ale nie a nie zbaviť. To je už fakt
podozrivé. Všimnime si, že tabuľka 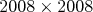 sa vyššie uvedeným spôsobom vyplniť dá tak, že v nej
nenájdeme inkriminovanú dvojicu. No a keby sa dala vyplniť aj naša
tabuľka, tak sa môžete staviť, že by zadávači použili tabuľku sa vyššie uvedeným spôsobom vyplniť dá tak, že v nej
nenájdeme inkriminovanú dvojicu. No a keby sa dala vyplniť aj naša
tabuľka, tak sa môžete staviť, že by zadávači použili tabuľku
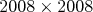 . Takže teraz vieme, že máme dokázať pravdivosť tvrdenia v
zadaní. . Takže teraz vieme, že máme dokázať pravdivosť tvrdenia v
zadaní.
Skúsime úlohu riešiť pre nejakú menšiu tabuľku s podobnými
vlastnosťami, ako má naša. Predošlé vyplnenie sa dá úspešne
zrealizovať pre rozmery tabuľky deliteľné štyrma, preto je
rozumné očakávať, že štvorka je perióda, s akou sa vlastnosti
tabuliek opakujú. Takže sa pozrime na tabuľku 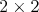 :) Vieme, že v nej bude jednotka a trojka. Taktiež vidíme, že
každé dve políčka tejto tabuľky spolu susedia, čo platí aj pre
jednotku a trojku pri ľubovoľnom vyplnení. Tvrdenie preto platí.
Vedeli by sme niečo z toho použiť aj na väčšie tabuľky? Veľmi
sľubne vyzerá tá časť o každých dvoch políčkach. Kým pre dve
políčka totiž máme jeden vzťah, pre tri už sú to tri vzťahy a
pre štyri dokonca až šesť. Bohužiaľ pre päť a viac políčok
už nenájdeme také plošné usporiadanie, aby každá dvojica
susedila, čo by mohlo veci komplikovať. Ale aj chlievik :) Vieme, že v nej bude jednotka a trojka. Taktiež vidíme, že
každé dve políčka tejto tabuľky spolu susedia, čo platí aj pre
jednotku a trojku pri ľubovoľnom vyplnení. Tvrdenie preto platí.
Vedeli by sme niečo z toho použiť aj na väčšie tabuľky? Veľmi
sľubne vyzerá tá časť o každých dvoch políčkach. Kým pre dve
políčka totiž máme jeden vzťah, pre tri už sú to tri vzťahy a
pre štyri dokonca až šesť. Bohužiaľ pre päť a viac políčok
už nenájdeme také plošné usporiadanie, aby každá dvojica
susedila, čo by mohlo veci komplikovať. Ale aj chlievik 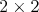 vyzerá veľmi schopne. Našu tabuľku vieme pekne rozdeliť na vyzerá veľmi schopne. Našu tabuľku vieme pekne rozdeliť na 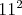 takýchto chlievikov. Čo sme tým dostali? Pretože políčka
chlievika susedia, tak pokiaľ v niektorom sú dve nuly, máme našu
dvojicu. Nech je teda v každom chlieviku práve jedna nula. Nech je
tiež po jednej dvojke v každom chlieviku, inak máme zase hľadanú
dvojicu. V chlievikoch ostávajú ešte po dve voľné miesta. takýchto chlievikov. Čo sme tým dostali? Pretože políčka
chlievika susedia, tak pokiaľ v niektorom sú dve nuly, máme našu
dvojicu. Nech je teda v každom chlieviku práve jedna nula. Nech je
tiež po jednej dvojke v každom chlieviku, inak máme zase hľadanú
dvojicu. V chlievikoch ostávajú ešte po dve voľné miesta.
V tomto momente by už malo byť vidieť, ako to dorazíme na
nesediacej parite. Ak to nevidíte, radšej na chvíľku nečítajte
ďalej a popremýšľajte. Ďaľší postup je len rutinný dôkaz, z
ktorého možno ideu nie je hneď vidieť. Okrem toho ho možno
previesť mnohými spôsobmi.
Ak by sa v žiadnom chlieviku nemiešali jednotky a trojky, tak by
v celej tabuľke bol párny počet jednotiek (lebo počet jednotiek v
nemiešanom chlieviku je párny). Ale my máme 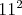 jednotiek, preto musí existovať miešaný chlievik, a to jedine
tak, že v ňom bude jedna jednotka a jedna trojka- a opäť máme
hľadanú dvojicu. Fertig. jednotiek, preto musí existovať miešaný chlievik, a to jedine
tak, že v ňom bude jedna jednotka a jedna trojka- a opäť máme
hľadanú dvojicu. Fertig. cituj ma |
|
|
 |
|
|



