|
|
 |
8. príklad 3. zimnej série 2009/2010
Zadanie:
Hovorí sa, že kto hľadá, nájde. V tejto úlohe máte nájsť
všetky trojice nezáporných celých čísel 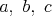 , pre ktoré platí , pre ktoré platí
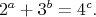
Nezabudnite zdôvodniť, prečo ďalšie trojice okrem nájdených už
neexistujú. |
IBnCB6Q0aE <8yqmbr37vvq~mail~com> - 01. 08. 2015 - 22:25:44 z 201-249-2-129.dyn.dsl.cantv.netHmm ..Good write-up, I am regular voiitsr of one's site, maintain up
the nice operate, and It is going to be a regular voiitsr for a
lengthy time. Our opinions do not really blossom into fruition until
we have expressed them to someone else. by Mark Twa cituj ma |
| škrečok - 14. 12. 2009 - 11:58:33 z 158.195.165.97peťo napísal:
Na olympiade by sa pouzitie tejto konkretnej vety
uznalo. |
... preto tam už príklady, ktoré sa dajú týmto vyriešiť,
nebudú dávať :)
cituj ma |
| peťo <peto~kms~sk> - 14. 12. 2009 - 00:17:40 z 158.195.169.177Na olympiade by sa pouzitie tejto konkretnej vety uznalo. cituj ma |
| Petržlen <petrzlen~kms~sk> - 10. 12. 2009 - 22:17:49 z 158.195.170.243HAgO napísal:
Pre neznavsich:
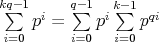
|
Konecne viem, co je to Hagova Transformacia :) (ked uz sa na nu
odvolavas), aj ked ta uprava bola v tom pripade dostatocne
pochopitelna.
cituj ma |
| Fillippo - 10. 12. 2009 - 10:17:22 z edunet-static-105.87-197-40.telecom.skeste by som sa vratil k teme: ci su povolene v olympiade a inych
sutaziach vety ako catalanova domnienka, velka fermatova veta,...
Udajne pokial sa nepovie inak, tak vsetko co ma meno, alebo sa vieme
odvolat na literaturu, kde je nieco dokazane, tak mozme pouzit ako
fakt. Takze pokial sa nepovedalo inak, tak by sa to malo uznat. napr.
minuly rok na vyberku pri jednom priklade vyslovene zakazali catalana,
tak tam to bolo jasne. aj ked zase pred dvoma rokmi ondro budac
neuznal riesenie s catalanom aj ked to nepovedal dopredu(odovodnil to
zase tym, ze vyberko nie je sutaz v pravom zmysle slova, ze ide o
vitaza, ale ze ide o to vybrat najschopnejsich ludi na IMO, ktory
vedia riesit priklady a nie ktory poznaju huste vety, alebo tak
nejak). mohli by sa kompetentni vyjadrit? mozno to je tema skor na
debatukms. teda ja si myslim, ze v skutocnej sutazi napr. kraj,
celostatko, imo, memo by to uznali, ale mozno pre ten ondrov dovod by
to neuznali v kms, alebo vyberku. cituj ma |
| HAgO - 02. 12. 2009 - 23:56:33 z chello089173091156.chello.skškrečok
napísal:
laciKE napísal:
co ja sa pamatam, tak na
vyberku pred dvoma rokmi sa to uznalo a jeden clovek dostal bod (mozno
aj dva) prave za spomenutie toho typka :D |
mali sme na výberku nejaký príklad, kde sa dala catalan's
conjecture použiť a rovno pred riešením sme vám povedali, že
tým sa to riešiť nemá, že vám body nedáme ;) celkovo je to moc
silné tvrdenie, v seminári na osmičku určite. ako ísť s
guľometom na muchu :) |
no akože myslím, že guľometom by som muchu netrafil...ale hentím
by som to vyriešil...
cituj ma |
| škrečok - 02. 12. 2009 - 08:07:10 z 158.195.166.204laciKE napísal:
co ja sa pamatam, tak na vyberku pred dvoma rokmi sa to uznalo a jeden
clovek dostal bod (mozno aj dva) prave za spomenutie toho typka
:D |
mali sme na výberku nejaký príklad, kde sa dala catalan's
conjecture použiť a rovno pred riešením sme vám povedali, že
tým sa to riešiť nemá, že vám body nedáme ;) celkovo je to moc
silné tvrdenie, v seminári na osmičku určite. ako ísť s
guľometom na muchu :)
cituj ma |
| |
| HAgO - 01. 12. 2009 - 22:19:11 z chello089173091156.chello.skmato napísal:
HAgO napísal:
ja
som pouzil HAgOvu transformaciu...dufam ze opravovatel ju
pozna... |
Na toto?
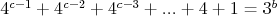 |
jop
cituj ma |
| mato - 01. 12. 2009 - 22:17:53 z dial-92-52-43-6-orange.orange.skHAgO napísal:
ja
som pouzil HAgOvu transformaciu...dufam ze opravovatel ju
pozna... |
Na toto?
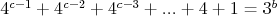
cituj ma |
| HAgO - 01. 12. 2009 - 21:11:06 z chello089173091156.chello.skja som pouzil HAgOvu transformaciu...dufam ze opravovatel ju pozna... cituj ma |
| laciKE - 01. 12. 2009 - 21:07:41 z nat-88-212-40-205.antik.skco ja sa pamatam, tak na vyberku pred dvoma rokmi sa to uznalo a jeden
clovek dostal bod (mozno aj dva) prave za spomenutie toho typka
:D
misof, to som si ani neuvedomil, ale scasti mas pravdu :D no nakoniec
som to predsa len nasiel, vo Filipovom prispevku, takze ta veta je
(mozno) pravdiva :D cituj ma |
| viktor.sz - 01. 12. 2009 - 20:02:04 z adsl-dyn229.78-98-0.t-com.sklaciKE napísal:
tak takto sa to vola :D nevedel som si spomenut, a po chvili hladania
v starych poznamkach som si povedal, ze asi bude lahsie dokazat tento
konkretny pripad ako najst to meno :D |
no aj tak ti to
laco bolo na nic,som sa pytal ci to mozem vyuzit a mi to zamietli...ze
v seminaroch na olympiadach ba aj na vyberkach to neuznavaju..daju ti
body nejake ale malo...
cituj ma |
| mišof - 01. 12. 2009 - 19:05:46 z dial-95-105-152-199-orange.orange.sklaco, tým si vlastne vyvrátil prvú vetu zadania :D cituj ma |
| laciKE - 01. 12. 2009 - 10:53:23 z nat-88-212-40-205.antik.sktak takto sa to vola :D nevedel som si spomenut, a po chvili hladania
v starych poznamkach som si povedal, ze asi bude lahsie dokazat tento
konkretny pripad ako najst to meno :D cituj ma |
| Fillippo <filip~sladek~gmail~com> - 01. 12. 2009 - 10:31:28 z edunet-static-105.87-197-40.telecom.skobvious, a=0. ze by sa tomu hovorilo catalan's conjecture, resp.
mihailescu's theorem? cituj ma |
|
|
 |
|
|



