Zadanie:
Ondro písal písomku z dejepisu, na ktorej bolo 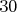 otázok. Pravidlá bodovania hovoria, že ak študent odpovie na otázok. Pravidlá bodovania hovoria, že ak študent odpovie na  otázok správne, na otázok správne, na 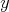 otázok nesprávne a na zvyšných otázok nesprávne a na zvyšných 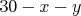 otázok sa rozhodne neodpovedať, dostane z písomky otázok sa rozhodne neodpovedať, dostane z písomky 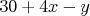 bodov. Ondrovi sa podarilo získať bodov. Ondrovi sa podarilo získať  bodov a hneď sa s tým pochválil Škrečkovi. Škrečok z tohto
počtu bodov dokázal zistiť, koľko mal Ondro správnych odpovedí.
Navyše si všimol, že keby Ondro získal ľubovoľný menší počet
bodov ako bodov a hneď sa s tým pochválil Škrečkovi. Škrečok z tohto
počtu bodov dokázal zistiť, koľko mal Ondro správnych odpovedí.
Navyše si všimol, že keby Ondro získal ľubovoľný menší počet
bodov ako  ale väčší ako ale väčší ako  , nedal by sa už počet jeho správnych odpovedí určiť
jednoznačne. Na koľko otázok z písomky odpovedal Ondro správne? , nedal by sa už počet jeho správnych odpovedí určiť
jednoznačne. Na koľko otázok z písomky odpovedal Ondro správne? |



