Zadanie:
V priestore je daná rovina 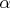 a priamka a priamka 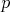 , ktorá leží v rovine , ktorá leží v rovine 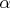 . Zvolíme v priestore bod . Zvolíme v priestore bod 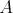 . Bod na priamke . Bod na priamke 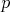 , ktorý je najbližšie k bodu , ktorý je najbližšie k bodu 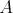 si označme si označme 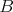 . Bod v rovine . Bod v rovine 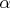 , ktorý je najbližšie k bodu , ktorý je najbližšie k bodu 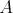 označme označme 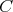 . Bod na priamke . Bod na priamke 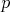 , ktorý je najbližší k bodu , ktorý je najbližší k bodu 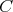 označme ako označme ako 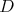 . Ako máme zvoliť bod . Ako máme zvoliť bod 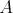 , aby vzdialenosť bodov , aby vzdialenosť bodov 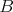 a a 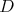 bola čo najväčšia? bola čo najväčšia?
|



