|
|
 |
14. príklad 3. letnej série 2009/2010
Zadanie:
Daný je kosoštvorec 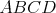 s vpísanou kružnicou s vpísanou kružnicou  . Vnútri uhla . Vnútri uhla 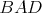 mimo kosoštvorca mimo kosoštvorca 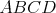 leží bod leží bod 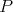 . Rovnobežka s priamkou . Rovnobežka s priamkou 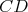 prechádzajúca bodom prechádzajúca bodom 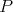 pretína priamku pretína priamku 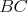 v bode v bode 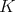 , rovnobežka s priamkou , rovnobežka s priamkou 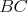 prechádzajúca bodom prechádzajúca bodom 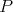 pretína priamku pretína priamku 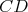 v bode v bode 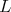 . Uvažujme z bodov . Uvažujme z bodov 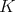 a a 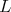 dotyčnice ku kružnici dotyčnice ku kružnici  rôzne od priamok rôzne od priamok 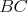 a a 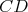 . Tieto dotyčnice sa pretínajú v bode . Tieto dotyčnice sa pretínajú v bode 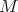 . Dokážte, že body . Dokážte, že body 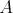 , , 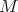 a a 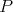 ležia na priamke. ležia na priamke. |
Fillippo - 24. 05. 2010 - 20:30:34 z ppp-77-234-226-61.dsidata.sktu elipsu som nasiel, ale povedal som si, ze elipsa nie je to, co sa
snazime najst na MO alebo v KMS, tak to asi nebude spravna cesta.
Kazdopadne pekne lemy, o ktorych som este nepocul a mozu sa zijst. cituj ma |
| Feráč - 23. 05. 2010 - 23:45:16 z worc-student-nat.worc.ox.ac.ukPodľa mňa veľmi pekný príklad. V zadaní sa spomínajú len
priamky a kružnice, v riešení (aspoň mojom) si ale treba do
obrázku dokresliť elipsu - človek si takto pripomenie, aká je to
užitočná krivka :)
Budeme potrebovať nasledovné vlastnosti dotyčníc k elipse. Sú to
celkom známe tvrdenia, možno ste sa s nimi stretli niekde na
deskriptívnej geometrii (ak sa to ešte stále učí), dajú sa
celkom dobre aj natipovať, keď viete, čo potrebujete.
Lemma 1: Ak 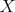 je bod na elipse je bod na elipse  s ohniskami s ohniskami 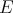 a a 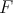 , tak dotyčnica k , tak dotyčnica k  prechádzajúca cez prechádzajúca cez 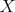 delí susedný uhol k uhlu delí susedný uhol k uhlu 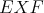 na polovicu. na polovicu.
Lemma 2: Ak  je elipsa so stredom je elipsa so stredom 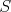 , , 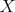 je bod vonku je bod vonku  a a 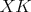 , , 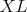 su dotyčnice k su dotyčnice k  ( (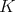 a a 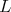 sú dotykové body), tak priamka sú dotykové body), tak priamka  delí úsečku delí úsečku 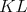 na polovicu (pre kružnicu to triviálne platí, celkom zaujímavé
ale je, že to platí aj pre elipsu). na polovicu (pre kružnicu to triviálne platí, celkom zaujímavé
ale je, že to platí aj pre elipsu).
No a teraz už dôkaz pôvodnej úlohy. Nech 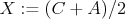 , , 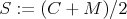 , , 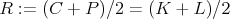 . Stačí dokázať, že . Stačí dokázať, že  sú kolineárne. sú kolineárne.
Tak ako vraví Filip, treba si porátať úseky dotyčníc z 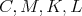 ku ku  . Napíšte si, ktoré vzdialensti sú rovnaké, a mali by ste dostať . Napíšte si, ktoré vzdialensti sú rovnaké, a mali by ste dostať
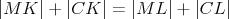 . To znamená, že . To znamená, že 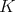 a a 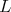 ležia na spoločnej elipse ležia na spoločnej elipse  s ohniskami s ohniskami 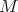 a a 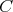 a stredom v a stredom v 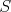 . Podľa Lemmy 1 sú . Podľa Lemmy 1 sú 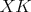 a a 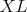 dotyčnice k dotyčnice k  . Potom podľa Lemmy 2 leží . Potom podľa Lemmy 2 leží 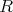 na na 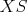 . . cituj ma |
| Fillippo - 19. 05. 2010 - 22:40:40 z ppp-77-234-226-61.dsidata.skco viac sa da robit okrem analytiky a ratanie usekov dotycnic? cituj ma |
|
|
 |
|
|



