Zadanie:
Hopko sa stratil v lese. Našťastie našiel rázcestie s názvom
\uv{Ortocentrum trojuholníka 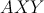 }. Vytiahol rýchlo mapu a začal hľadať, kde sa nachádza. Les má
tvar štvoruholníka }. Vytiahol rýchlo mapu a začal hľadať, kde sa nachádza. Les má
tvar štvoruholníka 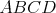 , v ktorom , v ktorom 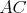 je os uhla je os uhla 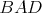 \linebreak a \linebreak a 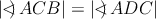 . Body . Body 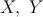 sú zaznačené ako päty výšok z bodu sú zaznačené ako päty výšok z bodu 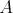 v trojuholníkoch v trojuholníkoch 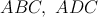 . Pomôžte Hopkovi zorientovať sa a dokážte, že ortocentrum
trojuholníka . Pomôžte Hopkovi zorientovať sa a dokážte, že ortocentrum
trojuholníka 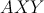 leží na priamke leží na priamke 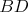 . .
|



