Zadanie:
Neprázdna množina 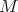 má má  prvkov. Označme prvkov. Označme 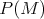 množinu všetkých podmnožín množiny množinu všetkých podmnožín množiny 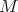 . Ďalej nech . Ďalej nech 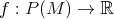 je funkcia, ktorá má nasledujúce vlastnosti:
\begin{enumerate}
\item[(i)] je funkcia, ktorá má nasledujúce vlastnosti:
\begin{enumerate}
\item[(i)] 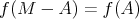 ,
\item[(ii)] ,
\item[(ii)] 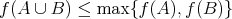 pre všetky pre všetky 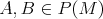 .
\end{enumerate}
Dokážte, že funkcia .
\end{enumerate}
Dokážte, že funkcia 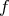 môže nadobúdať maximálne môže nadobúdať maximálne  rôznych hodnôt. rôznych hodnôt. |



