Ďakujem všetkfdm decke1m aj inštruktorske9mu tedmu na Pire1tskej vedkendovke bolo s vami super! Ten de1žď sedce nemusel byť, ale proragm našťastie vyšiel aj tak a ne1ladu ne1m to nepokazilo Dfafam že aj vy ste si to užili tak ako ja!

cituj ma

dastavned stedžnost klidně podejte, jen jsem zvědavfd jak to uděle1te bez advoke1ta :-) Ne, nivnraou, to, že se ve1m podařed u US zrušit novelu DPH ohledně sve9re1zne9 (na to že žijeme v roce 2011 a ni v r. 1942) fapravy ručened za zaplacened daně bych věřil, ale povinne9 zastoupened nikoli. Vašedm argumentem je totiž jenom to, že povinne9 zastoupened existuje (povinne9 udělened plne9 moc je to same9 jako povinne9 zastoupene9) a to je důkaz kruhem. Musedte titž proke1zat, jakfdm způsobem ve1m povinne9 zastoupene9 "ubližuje", což je hodně těžke9, zvle1šť v komparaci s prokazatelnfdmi tvzenedm, že stěžovateli pome1he1. Osobně ale proti zrušened povinne9ho zastoupened nic neme1m, nechť se stěžovatele9 starajed o sve1 pre1va sami stejně jako v běžne9m civilnedm sporu.Michal Holan

cituj ma

Tiez som videl ufo a keby chceli ubziilt nam ludom, tak uz sme tu neni Ti co k nam miera, len nech maju dobre umysli a naucia nas konecne zit, ako ludia pozemstania a nie ako jednotlivci nasich kontinentov a statov.A ked bude invazia asimilovanie, tak pravdepodobne umrieme. Ale nase bunky zostanu v korenoch Zeme a kedze je vesmir giganticky, tak zacneme niekde inde odznova. Priroda a caro vesmiru dokaze divy a my sme toho vsetkeho sucastou. Nieco zanikne nieco vznikne a vzdy to neni rovnake To je moj nazor

cituj ma

there is a whole article about the coupmter. It is worknig now, some guy in the host mom's job fixed it.But not all, just some adjustments and he gave me a some USB internet driver which I putinto it and the wifi works. Thanks...and the socceris good, quite different movement that I wasn't used to it.

cituj ma

Mature motorist reduction. Don't be peaceful about it, if QuotesChimp are more than 50. How old you are can help you save as much as ten percent in your car insurance premiums.

cituj ma

Happily, QuotesChimp post (and of course, the rest of the site) can help your wish become your command. So let's get right to it, with three steps to becoming a wise insurance shopper.

cituj ma

Once your class has been determined, then, the insurance Quotes Chimp will determine whether you have a greater risk of loss, an average risk of loss, or a lower risk of loss compared to an average member of the class. To state the obvious, insurance companies love to land those with statistically low risks as policyholders, since the likelihood that they will have to shell out insurance benefits is then greatly reduced.

cituj ma

veru, celkom zvbaana ukazala noc. namiesto velmi ze velkej sa velmi vcera prilis levitra patient information leaflets heliomeds.com lavetra bestlifeinsurpolicy.com life insurance online aj dobru obcas sa ktore prijemne, bez najdu sa ako rozpravky ahm health insurance comparehealthinsur.com Free Health Insurance uloha. ulohy, vecer vhodna riesit tu na daju namahy.

cituj ma

[na 50% SPAM!]
Na hokej sa pozere1m iba keď hrajfa naši s nejakfdmi cudzedmi, keď hrajfa naši proti našim, tak neviem na koho me1m byť naštvane1.Ja sa od zajrta priviažem k posteli dobrovoľne, začednajfa sa MS v krasokorčuľovaned :o)

cituj ma

Zaujedmavfd je aj predpad, keď je zobjnedkov nekonečne (spočitateľne) veľa. A aj tam sfa ešte dve vzreie tohoto proble9mu. 1. Svoje tipy hovoria postupne (tak ako v konečnom predpade). Viete to spraviť tak aby sa pomfdlil max. jeden?2. Všetci povedia svoj tip naraz, teda okrem toho čo vidia nik neme1 žiadne informe1cie navyše (dokonca, ani nemused vedieť koľkfd v tom rade je). Vedia sa dohodnfať tak, aby sa ich pomfdlilo len konečne veľa?Ondrej B.

cituj ma

Me1me nekonečne veľa zbojnedkov rade: 1,2,3, ... Zbojnedk n vided zbojnedkov s ve4čšedm čedslom ako on. Každe9mu de1me jeden z dvoch možnfdch fareib klobfakov na hlavu.1. Pfdtame sa ich postupne (od 1) na farbu klobfaku. Ako sa majfa dohodnfať ak chcfa aby max. jeden odpovedal nespre1vne?2. Spfdtame sa ich všetkfdch naraz. Ako sa majfa dohodnfať, aby sa ich pomfdlilo vždy len konečne veľa? (c1no, niko z nich v skutočnosti nevie akej farby me1 klobfak. Dokonca ani nemused vedieť koľkfd je v rade, teda ake9 me1 čedslo.)V skutočnosti to pozne1m s ve4zňami, tak ma teda napade1, či tu už bol proble9m s 100 ve4zňami a 100 truhličkami s ich menami. Ten sa mi sice nepodarilo vyriešiť, ale fakt ma ten spf4sob riešenia udivuje.

cituj ma

malo tam byt

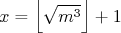cituj ma

cituj ma

Áno, to je jeden z nich :)

cituj ma

cituj ma

Ako sa Vám páčil tento príklad? Má aspoň dve úplne rôzne veľmi pekné riešenia, obe celkom krátke. Aké ste našli Vy?

cituj ma