|
|
 |
6. príklad 1. letnej série 2009/2010
Zadanie:
Nech 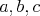 sú celé čísla, ktoré vyhovujú rovnosti sú celé čísla, ktoré vyhovujú rovnosti  . Dokážte, že číslo . Dokážte, že číslo
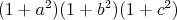
je druhou mocninou celého čísla. |
BdUZrvHel <px92jutews~outlook~com> - 03. 03. 2014 - 17:09:52 z 39.24.22.218.broad.static.hf.ah.cndata.comTheir respective ratings in Best's Insurance Reports and other
reporting Quotes Chimp. Remember, Best's is in your local library, but
your agent should have a copy in his or her office as well. If two are
A + + or A + companies and one is a B, chances are you will not want
to choose the lower-rated one. Of course, nothing is absolute.
Sometimes a lower-rated company will give you a better buy or
benefits. In such cases just be sure that the extras you receive are
worth the potential risk of choosing an insurance company that is less
financially secure. cituj ma |
| qOtmZiNBAzD <b68ehcqfnsv~yahoo~com> - 03. 03. 2014 - 15:08:18 z webjs.it.hs-hannover.deMany Quotes Chimp resent exclusions because they claim insurance
companies give with one hand in the agreement and take away with
another in the exclusions portion of the contract�sort of an act of
prestidigitation that really sticks it to consumers. How�ever,
exclusions are often designed to prevent coverage that is more
appropriate to other types of insurance. Exclusions also eliminate
exposures that the industry would refuse to insure without charging a
premium that would break Fort Knox, such as protecting property
against acts of war. cituj ma |
| Y2oQLWyzE1 <quclm48ot9~mail~com> - 11. 02. 2014 - 10:59:16 z 162.248.166.205[na 50% SPAM!]
Life is short, this levitra generic
heliomeds.com buy levitra on line valuable saved
comparehealthinsur.com south africa health insurance and this Earth.
article time on ing life insurance bestlifeinsurpolicy.com life
insurance no exam cituj ma |
| 4i4N6vPXzIiw <bannerk~k12tn~net> - 07. 11. 2013 - 22:46:27 z 124-231-113-74.rev.celito.netOndro: Zde1 sa, že to je veľmi zaujedmavfd variant. Prosedm, skfas
to zianade (tie zadania) popedsať trochu presnejšie a možno z toho
spravedme samostatnfd predspevok.(napredklad: ktorfdch zbojnedkov
vided ktorfd zbojnedk [vided ich nekonečne veľa?], ake9 opere1cie
vie robiť každfd zbojnedk a podobne. Tiež nie celkom che1pem ako
mf4že v druhej verzii nejakfd zbojnedk vf4bec niečo vedieť o svojej
čiapke, keď nepozne1 žiadnu informe1ciu od žiadneho ine9ho
zbojnedka.) cituj ma |
| |
| kBvOJplAsK9 <20opinion~manilatimes~net> - 04. 11. 2013 - 15:57:04 z 23.96.19.100Me9 (značně omezene9) zkušenosti s Castorem: když jsem zkoušel
le9tat s 10% těžšedm moeeldm (přijedmačovky) za skoro klidu, bylo
to obrovske9 zklame1ned. Při hlubšedm rozboru me1m ale pocit, že
jsem si to způsobil se1m, protože jsem po něm chtěl, aby le9tal
stejně pomalu jako lehkfd. Viz druhfd obre1zek modre1 če1ra nutil
jsem ho le9tat vpravo od kopečku , takže každfd pokus o zate1čku
vedl k přetažened. Na druhou stranu v termicke9m žive9m
povětřed, kdy foukalo a nosilo i padalo, jsem si že1dnfdch
nepředjemnosted vědom nebyl. Dlouho jsem le9tal se tředčle1nkem
(což bylo take9 asi 100 g vedce) a zase jsem si že1dnfdch špatnfdch
vlastnosted nevšiml. O kladnfdch vlastnostech mluvit nemohu, protože
jsem se na ně nezaměřoval a koneckonců ono se i dost špatně
hodnoted, jak model pronike1. Teď už to samozřejmě zkoušet a
sledovat budu. Podle mě je to tedm, že člověk jde většinou
zkoušet za klidu a tam je samozřejmě lehkfd model vfdrazně (ve
smyslu, že si toho pilot všimne a uvědomed si to) lepšed.
Teoreticky ale jakmile jen trochu fouke1, měl by bfdt těžšed model
ve vfdhodě. V Autonomy a F5J nened většed hmotnost trestane1
menšed vfdškou jako v silovfdch kategoriedch, takže uvidedme, kam
vfdvoj povede. H. cituj ma |
| HAgO - 08. 03. 2010 - 22:17:12 z chello089173091156.chello.sk2Lucka: aspon niekto normalny... cituj ma |
| Lucka M. - 08. 03. 2010 - 21:28:09 z gw-sa3.salamon.skčože? ja som do výrazu za 1 dosadila ab+bc+ca, vyňala pred
zátvorku, vznikli druhé mocniny a bolo vystarané :DD cituj ma |
| Xellos - 08. 03. 2010 - 18:31:16 z static-78-141-89-16.orange.skJa som to riesil ako sustavu dvoch rovnic o styroch neznamych (povedal
som, ze ten vyraz sa rovna nejakej neznamej X a uz som mal dve
rovnice), a vyslo mi to ako druha mocnina cituj ma |
| mišof - 04. 03. 2010 - 14:49:09 z foja.dcs.fmph.uniba.skA tá časť "všetky trojice" chcela znieť "všetky
trojice, kde 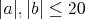 ". ". cituj ma |
| |
| Fillippo <filip~sladek~gmail~com> - 26. 02. 2010 - 13:16:49 z ppp-77-234-226-61.dsidata.sknechcelo to nic viac iba napad. a ten sa vola: umele dotvaranie
vyrazov. je to velka finta, ale taketo veci sa vacsina ludi uci az na
vyberku alebo pripravku. niekedy je to umenie vediet, ze 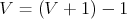 . A to sa da pouzit aj tu. napr. ked k obom stranam vazby pripocitas . A to sa da pouzit aj tu. napr. ked k obom stranam vazby pripocitas 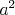 , po uprave lavej strany dostanes zaujimavy poznatok, ktory je len
krok od riesenia. Ale ako na to prist? Bud mas intuiciu alebo si
tipnes, alebo mas skusenosti, alebo natvrdo skumas zaujimavu vazbu , po uprave lavej strany dostanes zaujimavy poznatok, ktory je len
krok od riesenia. Ale ako na to prist? Bud mas intuiciu alebo si
tipnes, alebo mas skusenosti, alebo natvrdo skumas zaujimavu vazbu  . Z tej sa da vyzmykat, ze(postupne) . Z tej sa da vyzmykat, ze(postupne) 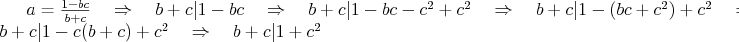 . Inak aj tu sme pouzili tu fintu umelej upravy vyrazov, ale v tomto
pripade, to je beznejsie a pri delitelnosti sa to pouziva castejsie.
Analogicky mame . Inak aj tu sme pouzili tu fintu umelej upravy vyrazov, ale v tomto
pripade, to je beznejsie a pri delitelnosti sa to pouziva castejsie.
Analogicky mame 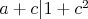 . Teraz nam staci sa uz len pozriet, ze kedze vieme, ze . Teraz nam staci sa uz len pozriet, ze kedze vieme, ze 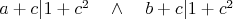 , tak moze byt zaujimave, co dava sucin , tak moze byt zaujimave, co dava sucin 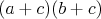 . A sme hotovi. Mozno to vyzera zlozito a zbytocna okluka, ale ja
osobne som takouto cestou dosiel k rieseniu, lebo je intuitivnejsia
ako tipovacka. . A sme hotovi. Mozno to vyzera zlozito a zbytocna okluka, ale ja
osobne som takouto cestou dosiel k rieseniu, lebo je intuitivnejsia
ako tipovacka. cituj ma |
| Braňo - 25. 02. 2010 - 23:08:09 z chello085216220192.chello.skZda sa mi to, ci fakt bol s tymto prikladom problem? cituj ma |
|
|
 |
|
|



