|
|
 |
12. príklad 1. letnej série 2009/2010
Zadanie:
Prirodzené číslo nazvime huňaté, ak žiadne prvočíslo v
jeho rozklade nemá exponent rovný jedna. Dokážte, že existuje
nekonečne veľa dvojíc po sebe idúcich prirodzených čísel,
ktoré sú obe huňaté. (Napríklad 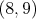 je taká dvojica.) je taká dvojica.) |
Fillippo <filip~sladek~gmail~com> - 01. 03. 2010 - 23:41:58 z ppp-77-234-226-61.dsidata.skdlho som nemal tusenie, co s tym robit a zacinalo mi to pripominat ten
pocit bezradnosti, ktory som zazival pri teorii cisel IMO 2008 3.
priklad. ale potom som si povedal, ze gama 12 nemoze byt taka hrozna.
takze poprve:stvorce su hunate a dobre s sa nimi robi. po druhe: ked
sa bavime o po sebe iducich cislach, tak ich rozdiel je jedna. Ale mi
predsa pozname vety z teorie cisel, ktore hovoria o rozdieloch
jedna(takyto pristup si myslim nesvedci moc matematikom: ze napasujme
vetu aby vyslo, tak to robia v skolach. No ale na MO sa moze aj ten
zist). Tie vety co ma napadli su: Catalan's conjecture (occasionally
now referred to as Mihăilescu's theorem), ale ta nam nepomoze, lebo
ta dokazuje neexistenciu veci, ktore su podobne tym, co chceme. Druha
je Pellova rovnica. A sme uz skoro na konci, lebo sucin hunatych cisel
je hunate cislo. ... QED cituj ma |
|
|
 |
|
|



