Zadanie 9. príkladu:
Miro má doma ostrouhlý trojuholník 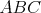 so stredom opísanej kružnice so stredom opísanej kružnice 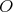 . Na jeho polpriamkach . Na jeho polpriamkach 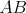 a a 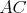 má postupne uložené body má postupne uložené body 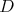 a a 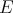 tak, že tak, že 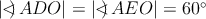 . Prezradil nám ešte, že štvoruholník . Prezradil nám ešte, že štvoruholník 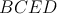 je tetivový. Čo za trojuholník má Miro doma? Dokážte, že Mirov
trojuholník je tetivový. Čo za trojuholník má Miro doma? Dokážte, že Mirov
trojuholník 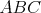 je rovnoramenný alebo je rovnoramenný alebo 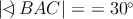 . .
|



