Zadanie 8. príkladu:
Čakanie na vyhlásenie výsledkov je zdĺhavé, tak sa Peťko
zahľadel na jeden pekný obraz a rozmýšľal, aké pekné veci
na ňom platia.\newline
Na obraze sa nachádza trojuholník 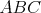 s bodom s bodom 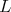 na strane na strane 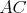 takým, že takým, že 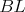 je os uhla je os uhla 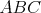 . Nech . Nech 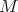 je ľubovoľný vnútorný bod úsečky je ľubovoľný vnútorný bod úsečky 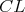 . Dotyčnica v bode . Dotyčnica v bode 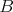 ku kružnici opísanej trojuholníku ku kružnici opísanej trojuholníku 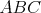 pretína polpriamku pretína polpriamku 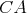 v bode v bode 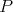 . Dotyčnice cez body . Dotyčnice cez body 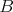 a a 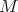 ku kružnici opísanej trojuholníku ku kružnici opísanej trojuholníku 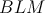 sa pretínajú v bode sa pretínajú v bode  . Dokážte, že priamka . Dokážte, že priamka  je rovnobežná s priamkou je rovnobežná s priamkou 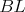 . .
|



