Zadanie 1. príkladu:
Maťo a Hago majú svoje obľubené čísla 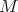 , , 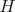 . Maťo má malú fantáziu, tak jeho obľubené číslo \textit{M} je
toľkociferné, aký je momentálne rok (teda momentálne je 2014
ciferné). Keďže Hago nemá fantáziu, tak jeho obľubené číslo
\textit{H} má presne rovnaké cifry ako \textit{M} len inak
usporiadané. Zrazu prišla Betka, a chcela zistiť, čo všetko
zvládnu spolu. Preto zisťovala súčet . Maťo má malú fantáziu, tak jeho obľubené číslo \textit{M} je
toľkociferné, aký je momentálne rok (teda momentálne je 2014
ciferné). Keďže Hago nemá fantáziu, tak jeho obľubené číslo
\textit{H} má presne rovnaké cifry ako \textit{M} len inak
usporiadané. Zrazu prišla Betka, a chcela zistiť, čo všetko
zvládnu spolu. Preto zisťovala súčet 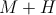 , a vyšlo jej číslo, ktorého cifry boli samé deviatky. Môžu
také , a vyšlo jej číslo, ktorého cifry boli samé deviatky. Môžu
také 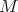 , , 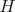 naozaj existovať? Mohlo by sa to stať o rok (t.j. ak naozaj existovať? Mohlo by sa to stať o rok (t.j. ak 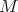 , , 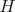 budú 2015-ciferné)? budú 2015-ciferné)?
|



