Zadanie 6. príkladu:
Nech 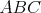 je pravouhlý trojuholník s pravým uhlom pri vrchole je pravouhlý trojuholník s pravým uhlom pri vrchole 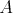 , pre ktorý platí , pre ktorý platí  . Nech . Nech 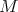 je stred strany je stred strany  , , 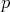 je kolmica na stranu je kolmica na stranu  prechádzajúca bodom prechádzajúca bodom 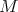 a a 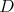 je priesečník priamky je priesečník priamky 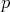 a úsečky a úsečky 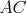 . Ďalej nech . Ďalej nech 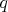 je kolmica na je kolmica na 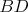 prechádzajúca bodom prechádzajúca bodom 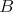 , ,  je rovnobežka s je rovnobežka s 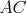 prechádzajúca bodom prechádzajúca bodom 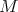 a a 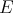 je priesečník je priesečník 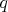 a a  . Dokážte, že trojuholníky . Dokážte, že trojuholníky 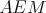 a a 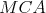 sú podobné práve vtedy, keď sú podobné práve vtedy, keď  . . |



